Ta có; 1110 = (10+1)10 ( khai triển nhị thức Niu- tơn )

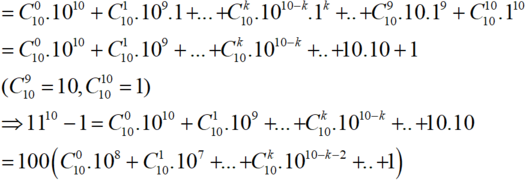
Do đó 1110 -1 chia hết cho 100

a, 6¹⁰⁰ - 1 = (6 . 6 . 6 ..... 6) - 1 = [(...6) . (...6) . (...6) ..... (...6)] - 1 = (...6) - 1 = ...5 \(⋮\) 5

b, 21²⁰ - 11¹⁰ = (21 . 21 . 21 . 21 . 21..... 21) - (11 . 11 . 11 . 11 ..... 11) = [(...1) . (...1) . (...1) . (...1).....(...1)] - [(...1) . (...1) . (...1) . (...1).....(...1)] = (...1) - (...1) = ....0 \(⋮\) 2; \(⋮\) 5

mình cảm ơn ạ

Hướng dẫn giải:

a) x chia hết cho 3 và 366 < x < 370:

x = 369.

b) x chia hết cho 9 và 1105 < x < 1110:

x = 1107.

a) Các số chia hết cho 5 là: 85; 1110; 9000; 2015; 3430.

b) Các số không chia hết cho 5 là: 56; 98; 617; 6714; 1053.

Lời giải:
Theo bài ra thì:

$x-6\vdots 9;x-9\vdots 15$

$\Rightarrow x-6-18\vdots 9; x-9-15\vdots 15$

$\Rightarrow x-24\vdots 9; x-24\vdots 15$

$\Rightarrow x-24$ là BC(9,15)

$\Rightarrow x-24\vdots BCNN(9,15)$

$\Rightarrow x-24\vdots 45$

$\Rightarrow x=45k+24$ với $k$ tự nhiên.

Theo đề ta cũng có: $x-7\vdots 11$

$\Rightarrow 45k+24-7\vdots 11$

$\Rightarrow 45k+17\vdots 11$

$\Rightarrow (44k+11)+(k+6)\vdots 11$

$\Rightarrow k+6\vdots 11$
Để $x$ nhỏ nhất thì $k$ cũng phải là stn nhỏ nhất. Do $k+6\vdots 11$ nên $k$ nhỏ nhất là $5$

Khi đó $x$ nhỏ nhất là: $5.45+24=249$

a: A=(1+4+4^2)+4^3(1+4+4^2)+...+4^21(1+4+4^2)

=21(1+4^3+...+4^21) chia hết cho 3

b: A=21(1+4^3+...+4^21)

mà 21 chia hết cho 7

nên A chia hết cho 7

c: A=(1+4+4^2+4^3)+4^4(1+4+4^2+4^3)+...+4^20(1+4+4^2+4^3)

=85(1+4^4+...+4^20) chia hết cho 17