Ta có; 1110 = (10+1)10 ( khai triển nhị thức Niu- tơn )
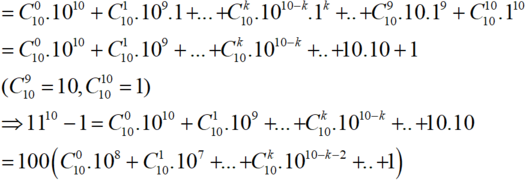
Do đó 1110 -1 chia hết cho 100
Ta có; 1110 = (10+1)10 ( khai triển nhị thức Niu- tơn )
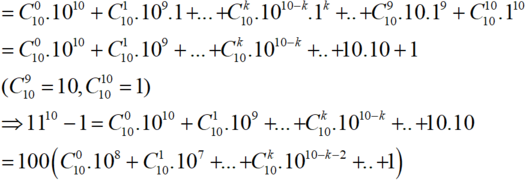
Do đó 1110 -1 chia hết cho 100
Chứng minh rằng: 101 100 – 1 chia hết cho 10000
Chứng minh rằng với n ∈ N * : 4 n + 15 n – 1 chia hết cho 9
Chứng minh rằng với mọi n ∈ N ∗ ta có 11 n + 1 + 12 2 n − 1 chia hết cho 133.
Chứng minh rằng với n ∈ N * : n 3 + 11 n chia hết cho 6.
Chứng minh rằng với n ∈ N * : n 3 + 3 n 2 + 5 n chia hết cho 3
Với mỗi số nguyên dương n, gọi u n = 9 n - 1 . Chứng minh rằng với mọi số nguyên dương n thì un luôn chia hết cho 8.
Chứng minh rằng với mọi n ∈ N ∗ ta có 2 n 3 − 3 n 2 + n chia hết cho 6
Chứng minh rằng Tổng các lập phương của ba số tự nhiên liên tiếp chia hết cho 9
Chứng minh với mọi n ∈ N * , ta có: 13 n – 1 chia hết cho 6