Cho các hàm số y=x-1 (d1); y=-x-3 và y =mx +m-1 (d3)
a) Tìm giá trị m để ba đường thẳng trên đồng quy
b) tính chu vi và diện tích của tam giác giới hạn (d1) và (d2) và trục hoành
c) Tìm khoảng cách từ gốc tọa độ đến (d1)
Cho hàm số y=x2
1. Cho các hàm số y = x + 2 và y=-x + m ( với m là tham số) lần lượt có đồ thị là (d) và (d1). Tìm tất cả các giá trị của m để trên 1 mặt phẳng tọa độ các đồ thị của (P),(d) (d1) cùng đi qua một điểm
G/s (P),(d),(d1) cùng đi qua một điểm
Gọi I(a,b) là giao điểm của (P),(d),(d1)
Có \(I\in\left(P\right),\left(d\right),\left(d1\right)\)\(\Rightarrow\left\{{}\begin{matrix}b=a^2\left(1\right)\\b=a+2\left(2\right)\\b=-a+m\left(3\right)\end{matrix}\right.\)
Từ (1);(2)\(\Rightarrow a^2=a+2\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-1\end{matrix}\right.\)
TH1: Tại \(a=2\Rightarrow b=a^2=4\)
Thay \(a=2;b=4\) vào (3) ta được:\(4=-2+m\) \(\Leftrightarrow m=6\)
TH2: Tại \(a=-1\Rightarrow b=a^2=1\)
Thay \(a=-1;b=1\) vào (3) ta được:\(1=1+m\) \(\Leftrightarrow m=0\)
Vậy m=6 hoặc m=0
Phương trình hoành độ giao điểm của (d) và (P):
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)(*)
Ta có: \(a-b+c=1-\left(-1\right)+\left(-2\right)=0\)
Do đó phương trình (*) có 2 nghiệm phân biệt
\(x_1=-1;x_2=\dfrac{-c}{a}=2\)
\(x_1=-1\) thì \(y_1=x_1^2=\left(-1\right)^2=1\)
\(x_2=2\) thì \(y_2=x_2^2=2^2=4\)
Vậy (d) và (P) cắt nhau tại 2 điểm phân biệt \(A\left(-1;1\right);B\left(2;4\right)\)
Do đó các đồ thị của (P), (d) và \(\left(d_1\right)\)cùng đi qua 1 điểm
\(\Leftrightarrow\left[{}\begin{matrix}A\in\left(d_1\right)\\B\in\left(d_1\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}1=1+m\\4=-2+m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\)
Vậy khi m=0 hoặc m=6 thì các đồ thị của (P),(d) và cùng đi qua 1 điểm
-Chúc bạn học tốt-
Cho hàm số y=x2 1. Cho các hàm số y = x + 2 và y=-x + m ( với m là tham số) lần lượt có đồ thị là (d) và (d1). Tìm tất cả các giá trị của m để trên 1 mặt phẳng tọa độ các đồ thị của (P),(d) (d1) cùng đi qua một điểm
Cho các hàm số:
y = 2x – 2 ( d 1 )
y = - (4/3).x – 2 ( d 2 )
y = (1/3).x + 3 ( d 3 )
Vẽ đồ thị các hàm số đã cho trên cùng một mặt phẳng tọa độ.
*Vẽ đồ thị hàm số y = 2x – 2 ( d 1 )
Cho x = 0 thì y = -2. Ta có: (0; -2)
Cho y = 0 thì 2x – 2 = 0 ⇔ 2x = 2 ⇔ x = 1. Ta có: (1; 0)
Đồ thị hàm số đi qua hai điểm (0; -2) và (1; 0)
*Vẽ đồ thị hàm số y = - (4/3).x – 2 ( d 2 )
Cho x = 0 thì y = -2. Ta có: (0; -2)
Cho y = 0 thì - (4/3).x – 2 = 0 ⇔ x = -1,5. Ta có: (-1,5; 0)
Đồ thị hàm số đi qua hai điểm (0; -2) và (-1,5; 0)
*Vẽ đồ thị hàm số y = (1/3).x + 3 ( d 3 )
Cho x = 0 thì y = 3. Ta có: (0; 3)
Cho y = 0 thì (1/3).x + 3 = 0 ⇔ x = -9. Ta có: (-9; 0)
Đồ thị hàm số đi qua hai điểm (0; 3) và (-9; 0)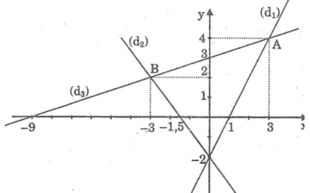
Cho các hàm số sau : y = 2x + 1 (D1) và y = x - 3 (D2)
a) Vẽ đồ thị của các hàm số trên cùng một mặt phẳng tọa độ
b) Tìm tọa độ giao điểm d1 và d2 bằng phép toán
c)Viết pt đường thẳng d3, biết d3//d1. Biết điểm A tọa độ (1,.,0) thuộc D3
a:
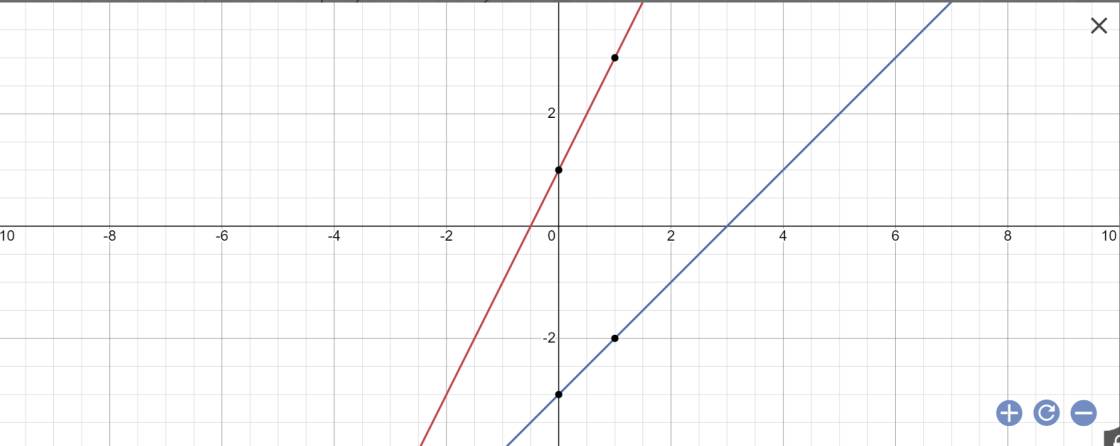
b: Phương trình hoành độ giao điểm là:
\(2x+1=x-3\)
=>\(2x-x=-3-1\)
=>x=-4
Thay x=-4 vào y=x-3, ta được:
\(y=-4-3=-7\)
Vậy: Tọa độ giao điểm của (D1) và (D2) là B(-4;-7)
c: Đặt phương trình đường thẳng (d3): y=ax+b
Vì (d3)//(d1) nên \(\left\{{}\begin{matrix}a=2\\b< >1\end{matrix}\right.\)
Vậy: y=2x+b
Thay x=1 và y=0 vào y=2x+b, ta được:
\(b+2\cdot1=0\)
=>b+2=0
=>b=-2
Vậy: (d): y=2x-2
Bài 1: (1,5đ) Cho hàm số y = – x + 1 có đồ thị là (d1)
và hàm số y = x – 2 có đồ thị là (d2)
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ Oxy.
b) Xác định các hệ số a, b của đường thẳng (d3): y = ax + b. Biết (d3) song song với (d1) và (d3) đi qua điểm A(3; 1).
Bài 2: Cho hàm số y= 1/2 x có đồ thị là (D1) và hàm số y= -x + 3 có đồ thị là (D2)
a) Vẽ (D1)) và (D2) trên cùng một mặt phẳng tọa độ
b) Cho đường thẳng (D3): y= ax + b. Xác định a, b, biết (D3) song song (D2) và cắt (D1)) tại điểm N có hoành độ bằng 4
Cho hàm số y=(5-2m)x+m-2, có đồ thị d1. Xác định m trong các trường hợp sau:
a) (d1) là hàm số bậc nhất
b) (d1) là hàm số đồng biến, nghịch biến
c) (d1) là đường thẳng đi qua gốc tọa độ
d) (d1) là đường thẳng song song với đồ thị y=-2x+5
e) (d1) là đường thẳng cắt trục tung tại điiểm có tung độ bằng -2, cắt trục hoành tại điểm có hoành độ bằng căn 3
1.Cho hàm số bậc nhất y= (m-1)x + 2m - 5 (d1)
a. Tính giá trị của m để đường thẳng (d1) song song với đường thẳng y= 3x+1 (d2)
b. Với giá trị nào của m thì đường thẳng (d1) và (d2) cắt nhau tại một điểm trên trục hoành
2. Cho các hàm số: y=2x+3, y=-x+2, y=2x2+1, y=\(\frac{1}{2}x\) - 2
a. Trong các hàm số trên, hàm số nào là hàm số bậc nhất?
b. Trong các hàm số bậc nhất tìm được ở câu a), hàm số nào đồng biến, hàm số nào nghịch biến trên tập hợp R? Vì sao
3.Xác địch hàm số bậc nhất y=ã+b biết đồ thị nó song song với đường thẳng y=2x-3 và cắt trục tung tại điểm có tung độ = 5
a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4
Cho các hàm số:
y = 2x – 2 ( d 1 )
y = - (4/3).x – 2 ( d 2 )
y = (1/3).x + 3 ( d 3 )
Tính khoảng cách AB
Ta có:
A B 2 = x A - x B 2 + y A - y B 2 = 3 + 3 2 + 4 - 2 2 = 40
AB = 40 = 2 10
Cho hàm số \(y=2x+4\) có đồ thị là (d1) và hàm số \(y=-x+1\) có đồ thị là (d2)
a. Vẽ (d1) và (d2) trên cùng một mặt phẳng toạ độ Oxy
b. Xác định các hệ số a, b của đường thẳng \(y=ax+b\) (d3). Biết (d3) song song với (d1) và (d3) cắt (d2) tại một điểm có hoành độ bằng 2
Bài 1: Cho hàm số có đồ thị là (D1) y = 1/2 x và hàm số có đồ thị là (D2) y= -x +3 a) Vẽ (D1)) và (D2) trên cùng một mặt phẳng tọa độ b) Cho đường thẳng (D3) y= ax +b: . Xác định a, b, biết (D3) song song (D2) và cắt (D1)) tại điểm N có hoành độ bằng 4
b: Thay x=4 vào (d1), ta được:
\(y=\dfrac{1}{2}\cdot4=2\)
Vì (d3)//(d2) nên a=-1
Vậy: (d3): y=-x+b
Thay x=2 và y=4 vào (d3), ta được:
b-2=4
hay b=6