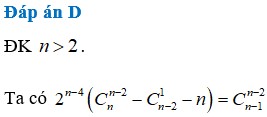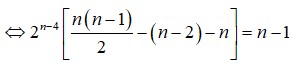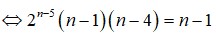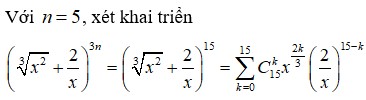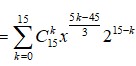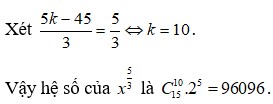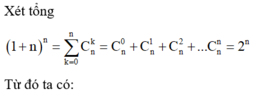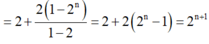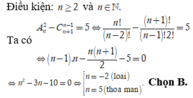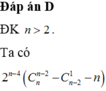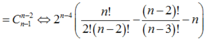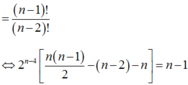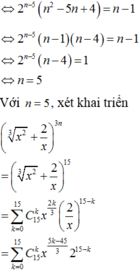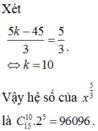Chứng minh: Cn+1n+4 = Cnn+3 + Cn+1n+3

Những câu hỏi liên quan
Gọi a là hệ số của
x
5
3
trong khai triển
(
x
2
3
+
2
x
)
3
n
,
x
0
biết rằng
2...
Đọc tiếp
Gọi a là hệ số của x 5 3 trong khai triển ( x 2 3 + 2 x ) 3 n , x > 0 biết rằng 2 n - 4 ( C n n - 2 - C n - 2 1 ) = C n - 1 n - 2
A. a = 96069
B. a = 96906
C. a = 96960
D. a = 96096
Có bao nhiêu số nguyên dương n sao cho
S
2
+
C
1
0
+
C
2
0
+
.
.
.
+
C
n
0...
Đọc tiếp
Có bao nhiêu số nguyên dương n sao cho S = 2 + C 1 0 + C 2 0 + . . . + C n 0 + C 1 1 + C 2 1 + . . . + C n 1 + . . . + C n - 1 n - 1 + C n n - 1 + C n n là một số có 1000 chữ số.
A. 3
B. 1
C. 0
D. 2
Có bao nhiêu số nguyên dương n sao cho
S
2
+
C
1
0
+
C
2
0
+
.
.
.
+...
Đọc tiếp
Có bao nhiêu số nguyên dương n sao cho
S = 2 + C 1 0 + C 2 0 + . . . + C n 0 + C 1 1 + C 2 1 + . . . + C n 1 + . . . + C n - 1 n - 1 + C n n - 1 + C n n
là một số có 1000 chữ số
A. 2.
B. 1.
C. 3.
D. 0.
Chọn đáp án C
Ta có
S = 2 + C 1 0 + C 2 0 + . . . + C n 0 + C 1 1 + C 2 1 + . . . + C n 1 + . . . + C n - 1 n - 1 + C n n - 1 + C n n
Xét khai triển
![]()
Thay x = 1 vào khai triển ta được
![]()
Suy ra
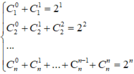
⇒ S = 2 + 2 1 1 - 2 n 1 - 2 = 2 n + 1
Số chữ số của S là
![]()
![]()
![]()
![]()
![]()
Do n ∈ Z nên n ∈ 3318 ; 3319 ; 3320 .
Vậy có 3 số nguyên dương n thỏa mãn yêu cầu bài toán
Đúng 0
Bình luận (0)
Tìm hệ số không chứa xx trong các khai triển sau (x3−2x)n(x3−2x)n, biết rằng Cn−1n+Cn−2n=78Cnn−1+Cnn−2=78 với x>0
Mình cần gấp giúp mình với ạ !!
Giải bất phương trình:
C
n
-
1
n
-
3
A
n
+
1
4
≤
1
14
P
3
A.
3...
Đọc tiếp
Giải bất phương trình: C n - 1 n - 3 A n + 1 4 ≤ 1 14 P 3
A. 3 ≤ n ≤ 7
B. n ≥ 7
C. 3 ≤ n ≤ 6
D. n ≥ 6
Giải bất phương trình
C
n
-
1
n
-
3
A
n
+
1
4
≤
1
14
P
3
Đọc tiếp
Giải bất phương trình C n - 1 n - 3 A n + 1 4 ≤ 1 14 P 3
![]()
![]()
![]()
![]()
Tìm giá trị n ∈ ℕ thỏa mãn A n 2 - C n + 1 n - 1 = 5
A. n = 3
B. n = 5
C. n = 4
D. n = 6
Gọi a là hệ số của
x
5
3
trong khai triển
x
2
3
+
2
x
3
n
,
x
0
biết rằng
2...
Đọc tiếp
Gọi a là hệ số của x 5 3 trong khai triển x 2 3 + 2 x 3 n , x > 0 biết rằng 2 n - 4 C n n - 2 - C n - 2 1 - n = C n - 1 n - 2
A. a = 96069
B. a = 96906
C. a = 96960
D. a = 96096
Tìm số nguyên dương n thỏa mãn các điều kiện sau
C
n
-
1
4
-
C
n
-
1
3...
Đọc tiếp
Tìm số nguyên dương n thỏa mãn các điều kiện sau C n - 1 4 - C n - 1 3 < 5 4 A n - 2 2 C n + 1 n - 4 ≥ 7 15 A n + 1 3
(Ở đây A n k , C n k lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử).
A. n=7
B. n=8
C. n=9
D. n=10
Tìm số nguyên dương n thỏa mãn các điều kiện sau
C
n
-
1
4
-
C
n
-
1
3...
Đọc tiếp
Tìm số nguyên dương n thỏa mãn các điều kiện sau
C n - 1 4 - C n - 1 3 < 5 4 A n - 2 2 C n + 1 n - 4 ≥ 7 15 A n + 1 3
(Ở đây A n k ; C n k lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử).
A. n = 7
B. n = 8
C. n = 9
D. n = 10
Điều kiện: n - 1 ≥ 4 nên n ≥ 5
Hệ điều kiện ban đầu tương đương:
⇔ n - 1 n - 2 n - 3 n - 4 4 . 3 . 2 . 1 - n - 1 n - 2 n - 3 3 . 2 . 1 ≤ 5 4 n - 2 n - 3 n + 1 n n - 1 n - 2 n - 3 5 . 4 . 3 . 2 . 1 ≥ 7 15 n + 1 n n - 1 ⇔ n 2 - 9 n - 22 < 0 n ≥ 5 n 2 - 5 n - 50 ≥ 0 ⇒ n = 10
Vậy n = 10 thỏa yêu cầu bài toán
Đáp án D
Đúng 0
Bình luận (0)