Tính giá trị biểu thức: P=(sin 2a+ tg^2a)/( cos a - cotg 2a) Khi a= 30 độ
B1 Rút gọn bt a:alphal
a) A= 1+sinacosa/cos^2a-Sin^2a)-(1+cotg^2a)(1-cos^2a)
b) B= (1+tg^2a)(1-Sin^2a)-(1+cotg^2a)(1-cos^2a)
Tìm giá trị của biểu thức S = \(\frac{cos^2a-sin^2b}{sin^2a.sin^2b}-cotg^2a.cotg^2b\)
\(S=\frac{cos^2a-sin^2b}{sin^2a.sin^2b}-cot^2a.cot^2b=\frac{cos^2a-sin^2b}{sin^2a.sin^2b}-\frac{cos^2a.cos^2b}{sin^2a.sin^2b}\)
\(=\frac{cos^2a-sin^2b-cos^2a.cos^2b}{sin^2a.sin^2b}=\frac{cos^2a-cos^2a.cos^2b-sin^2b}{sin^2a.sin^2b}\)
\(=\frac{cos^2a\left(1-cos^2b\right)-sin^2b}{sin^2a.sin^2b}=\frac{cos^2a.sin^2b-sin^2b}{sin^2a.sin^2b}\)
\(=\frac{sin^2b\left(cos^2a-1\right)}{sin^2a.sin^2b}=\frac{-sin^2a.sin^2b}{sin^2a.sin^2b}=-1.\)
1. Cho tam giác ABC vuông tại A, đường cao AH . Biết AH=6cm , HC - HB = 9cm. Tính các độ dài HB,HC.
2. Cho cos a = 0,28. Tính các giá trị lượng giác còn lại của góc a.
3. Tìm sin α, cos α biết:
a) tg α = \(\frac{3}{4}\) b) cotg α = \(\frac{5}{12}\)
4. Cho tan α = 4. Tính giá trị biểu thức
a) A= \(\frac{\sin a+\cos a}{\sin a-\cos a}\) b) B= \(\frac{3\sin^2a-3\cos^2a}{3\sin^2a-5\cos^2a}\)
Chứng minh rằng
a, \(tg^2a+1=\frac{1}{cos^2a}\)
b, \(cotg^2a+1=\frac{1}{sin^2a}\)
c, \(cos^4a-sin^4a=2cos^2a-1\)
a) \(\tan^2\alpha+1=\frac{\sin^2\alpha}{\cos^2\alpha}+1=\frac{\sin^2\alpha+\cos^2\alpha}{\cos^2\alpha}=\frac{1}{\cos^2\alpha}\)
b) \(\cot^2\alpha+1=\frac{\cos^2\alpha}{\sin^2\alpha}+1=\frac{\cos^2\alpha+\sin^2\alpha}{\sin^2\alpha}=\frac{1}{\sin^2\alpha}\)
c) \(\cos^4\alpha-\sin^4\alpha=\left(\cos^2\alpha+\sin^2\alpha\right)\left(\cos^2\alpha-\sin^2\alpha\right)=\cos^2\alpha-\sin^2\alpha\)
\(=2\cos^2\alpha-\left(\sin^2\alpha+\cos^2\alpha\right)=2\cos^2-1\)
Bài 1 : Cho biết sin=0,6. Tính cos, tg và cotg
Bài 2:
1. Chứng minh rằng
a) tg2 a+1=\(\dfrac{1}{cos^2a}\)
b) cotg2 a+1=\(\dfrac{1}{sin^2a}\)
c) cos4 a-sin4 a=2cos2 a-1
2. Áp dụng: tính sin, cos a, cotg a, biết tg a=2
Bài 3: Biết tg=4/3. Tính sin, cos, cotg
bài 1 : ta có : \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-sin^2x=1-\left(0,6\right)^2=\dfrac{16}{25}\)
\(\Rightarrow cosa=\pm\dfrac{4}{5}\)
\(\Rightarrow tanx=\dfrac{sinx}{cosx}=\pm\dfrac{3}{4}\) \(\Rightarrow cotx=\dfrac{1}{tanx}=\pm\dfrac{4}{3}\)
bài 2)
ý 1 : a) ta có : \(\dfrac{1}{cos^2a}=\dfrac{sin^2a+cos^2a}{cos^2a}=tan^2a+1\left(đpcm\right)\)
b) ta có : \(\dfrac{1}{sin^2a}=\dfrac{sin^2a+cos^2a}{sin^2a}=1+cot^2a\left(đpcm\right)\)
c) \(cos^4a-sin^4a=\left(sin^2a+cos^2a\right)\left(cos^2a-sin^2a\right)\)
\(=cos^2a-sin^2a=2cos^2a-cos^2a-sin^2a=2cos^2a-1\left(đpcm\right)\)
ý 2 :
ta có : \(tana=2\Rightarrow cota=\dfrac{1}{2}\)
ta có : \(tan^2a+1=\dfrac{1}{cos^2a}\Leftrightarrow cos^2a=\dfrac{1}{tan^2a+1}=\dfrac{1}{5}\)
\(\Rightarrow cosa=\pm\dfrac{1}{\sqrt{5}}\Rightarrow sin^2a=1-cos^2a=\dfrac{4}{5}\) \(\Rightarrow sina=\pm\dfrac{2}{\sqrt{5}}\)
vậy ............................................................................
bài 3 bạn tự luyện tập như bài 2 cho quen nha :)
cho tan a = 3 tính giá trị các biểu thức sau
a) \(A=\frac{\sin a.\cos a}{\sin^2a-\cos^2a}\)
b)
\(1+tan^2a=\frac{1}{cos^2a}\)
\(1+3^2=\frac{1}{cos^2a}\)
\(10=\frac{1}{cos^2a}\)
\(cos^2a=\frac{1}{10}\)
\(cosa=\pm\sqrt{\frac{1}{10}}\)
\(sin^2a+cos^2a=1\)
\(sin^2a+\frac{1}{10}=1\)
\(sin^2a=\frac{9}{10}\)
\(sina=+\sqrt{\frac{9}{10}}\)
Vì tan dương nên có hai trường hợp :
TH1 : cả sin và cos cùng dương :
\(A=\frac{sina\cdot cosa}{sin^2a-cos^2a}\)
\(=\frac{\sqrt{\frac{9}{10}}\cdot\sqrt{\frac{1}{10}}}{\frac{9}{10}-\frac{1}{10}}\)
\(=\frac{\frac{3}{10}}{\frac{8}{10}}\)
\(=\frac{3}{8}\)
TH2 : cả sin và cos cùng âm
\(A=\frac{sina\cdot cosa}{sin^2a-cos^2a}\)
\(=\frac{-\sqrt{\frac{9}{10}}\cdot-\sqrt{\frac{1}{10}}}{\frac{9}{10}-\frac{1}{10}}\)
\(=\frac{\frac{3}{10}}{\frac{8}{10}}\)
\(=\frac{3}{8}\)
Cho cos α = 1 3 . Tính giá trị của biểu thức P = sin 3 a - sin a sin 2 a
![]()
![]()

![]()
Chọn A.
Áp dụng công thức biến đổi tổng thành tích và công thức nhân đôi; ta có
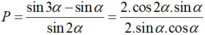

Chứng minh rằng:
a) \(\left(\dfrac{tga+cosa}{1+cotga.cosa}\right)^n=\dfrac{tg^na+cos^na}{1+cotg^na.cos^na},\forall n\in Z^+\)
b) \(tga.tgb=\dfrac{tga+tgb}{cotga+cotgb}\)
c) \(\dfrac{tg^2a-tg^2b}{tg^2a.tg^2b}=\dfrac{sin^2a-sin^2b}{sin^2a.sin^2b}\)
g) \(\dfrac{1}{4}\left(\sqrt{\dfrac{1+sina}{1-sina}}-\sqrt{\dfrac{1-sina}{1+sina}}\right)^2=tg^2a\)
cho tam giác ABC tìm giá trị lớn nhất của biểu thức:
(sin^2A+sin^2B+sin^2C)/(cos^2A+cos^2B+cos^2C)
