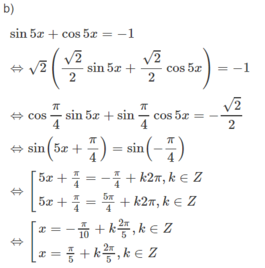tập giá trị hàm số y=cos5x-sin5x

Những câu hỏi liên quan
Tập giá trị của hàm số y=cos5x-sin5x là
Lời giải:
Áp dụng BĐT Bunhiacopxky:
$y^2=(\cos 5x-\sin 5x)^2\leq (\cos ^25x+\sin ^25x)(1+1)=2$
$\Rightarrow -\sqrt{2}\leq y\leq \sqrt{2}$
Vậy TGT của $y$ là $[-\sqrt{2}; \sqrt{2}]$
Đúng 2
Bình luận (0)
\(y=cos5x-sin5x=\sqrt{2}cos\left(5x+\dfrac{\pi}{4}\right)\)
Do \(-1\le cos\left(5x+\dfrac{\pi}{4}\right)\le1\)
nên \(-\sqrt{2}\le\sqrt{2}cos\left(5x+\dfrac{\pi}{4}\right)\le\sqrt{2}\)
và ta có \(-\sqrt{2}\le y\le\sqrt{2}\)
Tập giá trị : \(T=\left[-\sqrt{2};\sqrt{2}\right]\)
Đúng 0
Bình luận (0)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
sin
5
x
+
3
cos
x
. Trong các mệnh đề sau mệnh đề nào là sai? A. M + m 0 B. Mn -3 C. M - m
2
3
D.
M
m
1
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin 5 x + 3 cos x . Trong các mệnh đề sau mệnh đề nào là sai?
A. M + m = 0
B. Mn = -3
C. M - m = 2 3
D. M m = 1
Chọn D

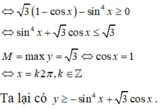
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có
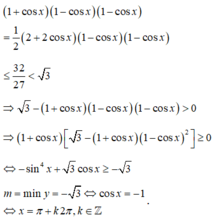
Do đó 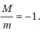 . Vì vậy, mệnh đề D sai.
. Vì vậy, mệnh đề D sai.
Đúng 0
Bình luận (0)
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
sin
5
x
+
3
cos
x
. Trong các mệnh đề sau mệnh đề nào là sai? A. M + m 0 B. Mm -3 C. M - m
2
3
D.
M
m
1
Đọc tiếp
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sin 5 x + 3 cos x . Trong các mệnh đề sau mệnh đề nào là sai?
A. M + m = 0
B. Mm = -3
C. M - m = 2 3
D. M m = 1
Ta có
sin 5 x ≤ sin 4 x ⇒ y ≤ sin 4 x + 3 cos x
Áp dụng bất đẳng thức Cauchy ta có:
1 - cos x 1 + cos x 1 + cos x = 1 2 2 - 2 cos x 1 + cos x 1 + cos x
≤ 1 2 2 - 2 cos x + ( 1 + cos x ) 2 3 3 = 32 27 < 3
⇒ 3 - 1 - cos x 1 + cos x 2 > 0 ⇒ 1 - cos x 3 - 1 - cos x 1 + cos x 2 ≥ 0 ⇒ 3 1 - cos x - sin 4 x ≥ 0 ⇔ sin 4 x + 3 cos x ≤ 3
M = maxy = 3 ⇔ cos(x) = 1
⇔ x = k 2 π , k ∈ ℤ
Ta lại có
y ≥ - sin 4 x + 3 cos x
Tương tự như trên, áp dụng bất đẳng thức Cauchy ta có:
1 + cos x 1 - cos x 1 - cos x = 1 2 2 + 2 cos x 1 - cos x 2 ≥ 32 27 ≤ 3 ⇒ 3 - 1 + cos x 1 - cos x 2 > 0 ⇒ 1 + cos x 3 - 1 + cos x 1 - cos x 2 ⇔ sin 4 x + 3 cos x ≥ - 3 m = m i n y = - 3 ⇔ cos x = - 1 ⇔ x = k 2 π , k ∈ ℤ
Do đó M m = - 1 . Vì vậy, mệnh đề D sai.
Đáp án cần chọn là D
Đúng 0
Bình luận (0)
Kí hiệu M và m theo thứ tự là giá trị lớn nhất và nhỏ nhất của hàm số
y
sin
3
x
+
cos
5
x
. Khi đó
M
-
m
bằng A. 0 B. 1 C. 2 D. 4
Đọc tiếp
Kí hiệu M và m theo thứ tự là giá trị lớn nhất và nhỏ nhất của hàm số y = sin 3 x + cos 5 x . Khi đó M - m bằng
A. 0
B. 1
C. 2
D. 4
Chọn C.
Dễ thấy
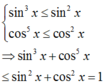
Đẳng thức xảy ra khi và chỉ khi
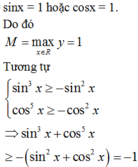
Đẳng thức xảy ra khi và chỉ khi sin x = - 1 hoặc cos x = - 1
Do đó
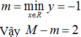
Đúng 0
Bình luận (0)
Tìm tập xác định hàm số
y=căn cos5x +1
y=\(\sqrt{cos5x+1}\)
dk : cos5x+1\(\ge\)0
<=> 1\(\ge\)cos5x\(\ge\)-1
<=>\(\frac{k2\pi}{5}\) \(\le\)x\(\le\)\(\frac{\pi}{5}+\frac{k2\pi}{5}\). k thuoc Z
Đúng 0
Bình luận (0)
Giải PTa1) dfrac{left(1-2sin xright)cos x}{left(1+2sin xright)left(1-sin xright)}sqrt{3}a2) 2sin17x+sqrt{3}cos5x+sin5x0a3) cos7x-sin5xsqrt{3}left(cos5x-sin7xright)a4) sqrt{3}cos5x-2sin3xcos2x-sin x0a5) tan x+cot x2left(sin2x+cos2xright)
Đọc tiếp
Giải PT
a1) \(\dfrac{\left(1-2\sin x\right)\cos x}{\left(1+2\sin x\right)\left(1-\sin x\right)}=\sqrt{3}\)
a2) \(2\sin17x+\sqrt{3}\cos5x+\sin5x=0\)
a3) \(\)\(\cos7x-\sin5x=\sqrt{3}\left(\cos5x-\sin7x\right)\)
a4) \(\sqrt{3}\cos5x-2\sin3x\cos2x-\sin x=0\)
a5) \(\tan x+\cot x=2\left(\sin2x+\cos2x\right)\)
Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) 5cosx - cos5x trên đoạn
-
π
3
;
π
3
. Tính Mm A.
6
3
B. 8 C.
12
3
D.
3
3
Đọc tiếp
Gọi M,m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f(x) = 5cosx - cos5x trên đoạn - π 3 ; π 3 . Tính Mm
A. 6 3
B. 8
C. 12 3
D. 3 3
f ' x = - 5 sin x + 5 sin 5 x = 10 cos 3 x sin 2 x f ' x = 0 ⇔ sin 2 x = 0 cos 3 x = 0 ⇔ x = k π 2 x = π 6 + k π 3
Do x ∈ - π 3 ; π 3 nên x ∈ - π 6 ; 0 ; π 6 . Ta có
f - π 3 = f π 3 = 2 f - π 6 = f π 6 = 3 3 f 0 = 4
Suy ra M = 3 3 ; m = 2. Vậy Mm = 6 3
Đáp án A
Đúng 0
Bình luận (0)
Giải các phương trình sau sin5x + cos5x = -1
tìm tập xác định của hàm số
\(y=\frac{\tan x+3}{sin5x}\)