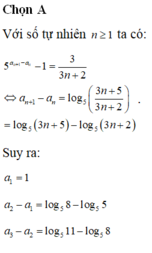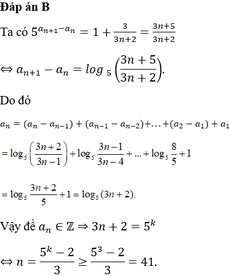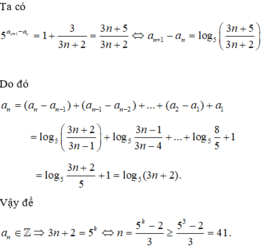Tìm số nguyên k sao cho 36n-1 - k . 33n-2 + 1 chia hết cho 7 với mọi số nguyên dương n

Những câu hỏi liên quan
tìm số nguyên k sao cho 36n-1-k.33n-2+1 chia hết cho 7 với mọi số nguyên dương n.
MN GIÚP MIK VS NHANH NHANH NHA
Ta thấy :
36n-1 - k . 33n-2 + 1 ⋮ 7 <=> 9 . ( 36n-1 - k . 33n-2 + 1 ) ⋮ 7
<=> 36n+1 - k . 33n + 9 ⋮ 7
Vì 36n+1 ≡ 3 ( mod 7 ) , suy ra 36n+1 + 9 ≡ 5 ( mod 7 )
Do đó để 36n+1 - k . 3 + 9 ⋮ 7 thì k . 33n ≡ 5 ( mod 7 )
Từ đó ta chứng minh được : Nếu n chẵn thì k ≡ 5 ( mod 7 ) , còn nếu lẻ thì k ≡ -5 ( mod 7 )
Tìm các số nguyên dương n lẻ sao cho n-1 là số nguyên dương nhỏ nhất trong các số nguyên dương k thỏa mãn \(\frac{k\left(k+1\right)}{2}\)chia hết cho n
Với mọi số nguyên dương n≥3 và mọi số nguyên dương k, chứng minh rằng:
n k không chia hết cho n-1.
n k -1 chia hết cho n-1
Thử ha! Lâu không làm quên mất cách làm rồi má ơi:((
Giả sử \(n^k⋮n-1\left(1\right)\Rightarrow n⋮n-1\) Vì:
Nếu n không chia hết cho n - 1 thì khi phân tích ra thừa số nguyên tố, n không chứa n - 1 nên nk cũng không chưa thừa số nguyên tố n - 1 suy ra nk không chia hết cho n - 1. Mâu thuẫn với điều giả sử (1)
Vậy \(n⋮n-1\Leftrightarrow\left(n-1\right)+1⋮\left(n-1\right)\Rightarrow1⋮\left(n-1\right)\)
Suy ra \(n-1\inƯ\left(1\right)=1\left(\text{không xét }-1\text{ vì n\ge3 nên }n-1\text{dương. Do vậy ta chỉ xét ước dương}\right)\Rightarrow n=2\)
Mà n = 2 không thỏa mãn đk nên không tồn tại n > 3 thỏa mãn n chia hết cho n - 1 tức là không tồn tại nk chia hết cho n - 1 (mẫu thuẩn với điều giả sử)
Do vậy ta có đpcm.
P/s: Sai thì thôi nhá, quên mất cách làm mọe rồi
Đúng 0
Bình luận (0)
nk-1=(n-1)(nk-1-nk-2....+1) chia hết cho n-1
Cho dãy số
(
a
n
)
thỏa mãn
5
a
n
+
1
-
a
n
3
3
n
+
2
với mọi n
≥...
Đọc tiếp
Cho dãy số ( a n ) thỏa mãn 5 a n + 1 - a n = 3 3 n + 2 với mọi n ≥ 1. Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Chọn A
Với số tự nhiên n ≥ 1, ta có:
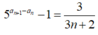
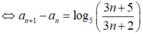
![]()
Suy ra:
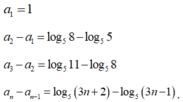
Cộng tương ứng hai vế các đẳng thức trên ta có ![]() với mọi số tự nhiên n
≥
1
với mọi số tự nhiên n
≥
1
Để ![]()
![]()
Ta kiểm tra với các giá trị k ∈ ℕ từ bé đến lớn
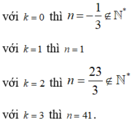
Vậy số nguyên n > 1 nhỏ nhất là n = 41( ứng với k = 3).
Đúng 0
Bình luận (0)
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
3
3
n
+
2...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Cho dãy số
(
a
n
)
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
-
1
3
3
n...
Đọc tiếp
Cho dãy số ( a n ) thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 49
B. n = 41
C. n = 123
D. n = 39
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
-
1
3
3
n...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 với mọi n ≥ 1 Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên.
A. n = 49
B. n = 41
C. n = 123
D. n = 39
Cho dãy số
a
n
thỏa mãn
a
1
1
và
5
a
n
+
1
-
a
n
-
1
3
3
n...
Đọc tiếp
Cho dãy số a n thỏa mãn a 1 = 1 và 5 a n + 1 - a n - 1 = 3 3 n + 2 , với mọi n ≥ 1 . Tìm số nguyên dương n > 1 nhỏ nhất để a n là một số nguyên
A. n = 41
B. n = 39
C. n = 49
D. n = 123
Tìm tất cả các số nguyên dương k sao cho tồn tại số nguyên dương n thỏa mãn 2n+11 chia hết cho 2k-1.
Để tìm tất cả các số nguyên dương k thỏa mãn điều kiện đã cho, ta sẽ giải phương trình theo n.
2n + 11 chia hết cho 2k - 1 có nghĩa là tồn tại một số nguyên dương m sao cho:
2n + 11 = (2k - 1)m
Chuyển biểu thức trên về dạng phương trình tuyến tính:
2n - (2k - 1)m = -11
Ta nhận thấy rằng nếu ta chọn một số nguyên dương nào đó, ta có thể tìm được một số nguyên dương k tương ứng để phương trình trên có nghiệm. Do đó, ta chỉ cần tìm tất cả các số nguyên dương n thỏa mãn phương trình trên.
Để giải phương trình này, ta có thể sử dụng thuật toán Euclid mở rộng (Extended Euclidean Algorithm). Tuy nhiên, trong trường hợp này, ta có thể tìm được một số giá trị n và k thỏa mãn phương trình bằng cách thử từng giá trị của n và tính giá trị tương ứng của k.
Dưới đây là một số cặp giá trị n và k thỏa mãn phương trình đã cho:
(n, k) = (3, 2), (7, 3), (11, 4), (15, 5), (19, 6), …
Từ đó, ta có thể thấy rằng có vô số giá trị n và k thỏa mãn phương trình đã cho.
Đúng 0
Bình luận (1)