Cho tam giác ABC vuông tại A các điểm D,e thuộc BC sao cho BD=DE=EC biết AD=10 AE=15 Tính BC

Những câu hỏi liên quan
Cho tam giác abc vuông tại a. các điểm d,,e thuộc bc sao cho bd=de=ec. biết ad=10 cm , ae=15 cm. tính bc ?
Cho tam giác ABC vuông tại A. Các điểm D, E thuộc cạnh BC sao cho BD=DE=EC. Biết AD=10cm, AE=15cm. Tính BC
Cho tam giác ABC vuông tại A, lấy các điểm D và E thuộc cạnh BC sao cho BD=DE=EC. Biết AD=10cm, AE=15cm. Tính độ dài BC.
cho tam giác ABC vuông tại A , các điểm D,E thuộc BC sao cho BD=DE=EC.biết AD=10, AE=15.tính bc
bài 10 Cho tam giác ABC cân tại A . Trên cạnh BC lấy các điểm BC lấy điểm D và E sao cho : BD=DE=EC. Gọi M là trung điểm của DE . 1) chứng minh AM vuông góc BC . 2) So sánh các độ dài AB,AD,AE,AC
a) Ta có: (hai góc kề bù)
(hai góc kề bù)
mà (hai góc ở đáy của ΔABC cân tại A)
nên
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Ta có: AD=AE(cmt)
nên A nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MD=ME(M là trung điểm của DE)
nên M nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của DE
hay (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác abc cân tại a. Trên tia bc lấy điểm d và e sao cho bd=de=ec. M là trung điểm de.
A, chứng minh am vuông góc với bc
B, so sánh ab,ad,ac,ae
Xem chi tiết
a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔABC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: AD=AE(hai cạnh tương ứng)
Ta có: AD=AE(cmt)
nên A nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MD=ME(M là trung điểm của DE)
nên M nằm trên đường trung trực của DE(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của DE
\(\Leftrightarrow AM\perp DE\)
hay \(AM\perp BC\)(đpcm)
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A (A>90độ) trên cạnh BC lấy 2 điểm D,E sao cho BD=DE=EC. Kẻ BH vuyoong góc với AD,CK vuông góc với AE(H thuộc AD,K thuộc AE)BH cắt CK tại G.CMR a) tam giác ADE cân b)BH=CK C) Gọi M là trung điểm của BC .CM A,M,G thẳng hàng d)AC>AD e)DAE>DAB
vote cho tui nha
Cho tam giác ABC có AB AC. Lấy hai điểm D, E thuộc cạnh BC sao cho BD DE EC. Biết AD AE.a) Chứng minh
E
A
B
^
D
A
C
^
.b) Gọi M là trung điểm của BC. Chúng minh AM là phân giác của
D
A
E
^
c) Giả sử
D
A
E...
Đọc tiếp
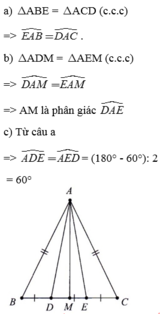
Cho tam giác ABC có AB = AC. Lấy hai điểm D, E thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE.
a) Chứng minh E A B ^ = D A C ^ .
b) Gọi M là trung điểm của BC. Chúng minh AM là phân giác của D A E ^
c) Giả sử D A E ^ = 60 ° . Tính các góc còn lại của tam giác DAE.
Cho tam giác ABC cân tại A. Trên cạnh BC lấy các điểm D và E. sao cho BD = DE = EC. Gọi M là trung điểm của DE
a, Chứng minh rằng AM vuông BC
b, So sánh cá độ dài AB, AD,AE,AC
a) xét 2 tam giác vuông ABM VÀ ACM, có:
AB=AC ( ABC CÂN)
góc b = góc c (___nt____)
BM=CM ( BD=EC; DM=ME)
=> TAM GIÁC ABM = T/GIÁC ACM
=>góc amb = góc amc (2 góc tuog ứng)
mà amb và amc là 2 góc kề bù
=> amb = amc = 90 độ hay am vuông góc với bc
b) ta có ab = ac vì t/giác abc cân tại a
xét t/giác adm và t/giác ame, có
am chung
góc amd=góc ame (cmt)
dm=me ( gt)
=> t/giác ADM = t/giác AME
=> AD=AE ( 2 cạnh tương ứng )
Đúng 0
Bình luận (1)
a, \(\Delta AMB=\Delta AMC(c.c.c)\Rightarrow\widehat{AMB}=\widehat{AMC}\)
Ta lại có : \(\widehat{AMB}+\widehat{AMC}=180^0\)=> \(\widehat{AMB}=90^0\)
Vậy \(AM\perp BC\)
b, Hình chiếu MD = ME nên đường xiên AD = AE . Hình chiếu MD < MB nên đường xiên AD < AB . Ta có : AD < AB = AC
Đúng 1
Bình luận (0)