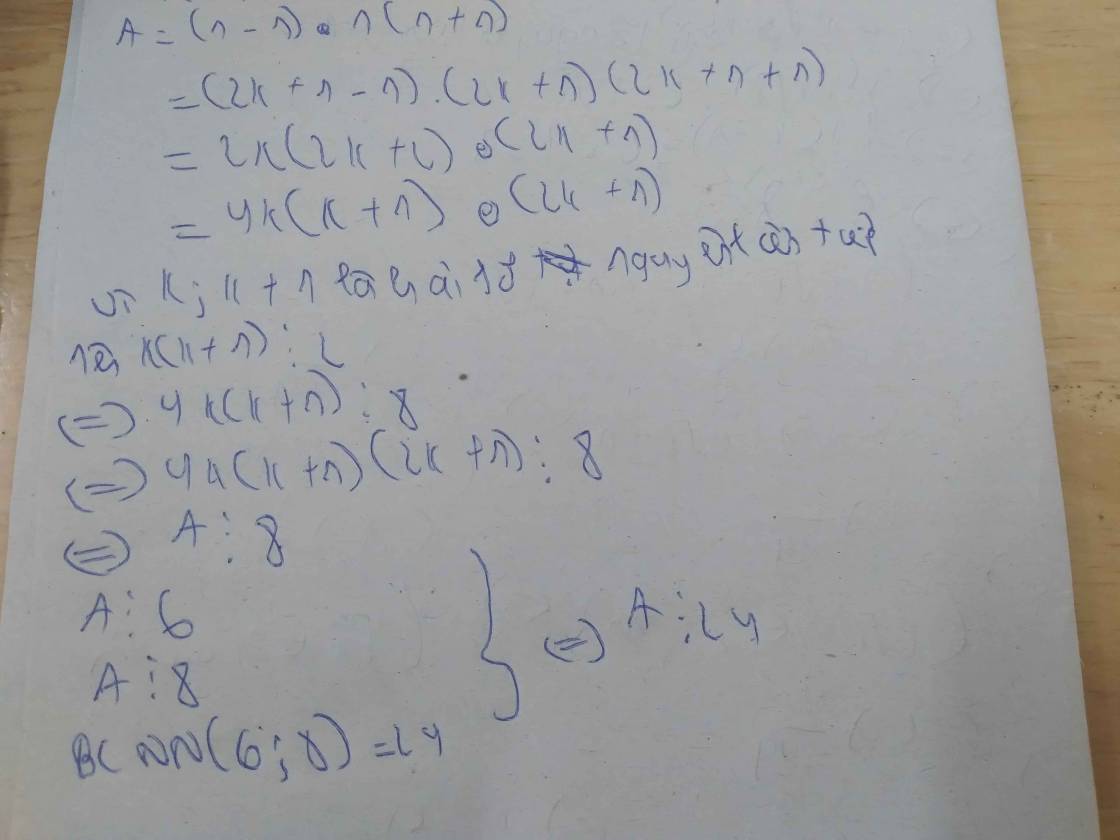CMR: 1<\(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{a+c}< 2\)

Những câu hỏi liên quan
Sử Dụng phương pháp qui nạp để giải:
1)CMR:9^2n+14 chia hết cho 5.
2)CMR:16^n-15n-1 chia hết cho 225.
3)CMR:4^n+15n-1 chia hết cho 9.
4)CMR:1+2+...+n=n(n+1)/2
5)CMR:11^n+1+12^2n-1 chia hêts cho 133
Ai xong nhanh nhất , chi tiết nhất tự biết rồi đấy!
Mình sẽ tích cho
a, Với n lẻ cmr A= (n-1) n (n+1) ⋮ 24
b,Với n lẻ cmr n2 - 1 ⋮ 8
a)Cho A= 1/2^2+1/3^2+...+1/n^2.CMR A<1
b)Cho B=1/2^2+1/4^2+1/6^2+...+1/(2n)^2.CMR B<1/2
c)Cho C=3/4+8/9+15/16+...+n^2-1/n^2.CMR C<n-2
Câu 1 : CMR (n-1)! chia hết n thì n là SNT
Câu2: CMR 100! không chia hết 2^100
Câu 3: CMR 1300! chia hết 169^53
Cho x>y TM: x+y<=1 CMR: 1/x^2+y^2 = 1/xy>=6
Cho a,b,c >0 TM: a+b+c<=1 CMR: (1/a^2+bc) + (1/b^2+ac)+ 1/c^2+2ab >=9
Cho a,b>0 TM: a+b<=1 ;CMR: (1/a^b^2)+4b+1/ab>=7
Cho a,b>0 TM:a+b<=1. CMR: 1/1+a^2+b^2 +1/2ab >=8/3
Cho a,b,c>0 TM: a+b+c<=3.CMR: 1/a^2+b^2+c^2 +2009/ab+bc+ac >=670
Cho x>y TM: x+y<=1 CMR: 1/x^2+y^2 = 1/xy>=6
Cho a,b,c >0 TM: a+b+c<=1 CMR: (1/a^2+bc) + (1/b^2+ac)+ 1/c^2+2ab >=9
Cho a,b>0 TM: a+b<=1 ;CMR: (1/a^b^2)+4b+1/ab>=7
Cho a,b>0 TM:a+b<=1. CMR: 1/1+a^2+b^2 +1/2ab >=8/3
Cho a,b,c>0 TM: a+b+c<=3.CMR: 1/a^2+b^2+c^2 +2009/ab+bc+ac >=670
Cho x>y TM: x+y<=1 CMR: 1/x^2+y^2 = 1/xy>=6
Cho a,b,c >0 TM: a+b+c<=1 CMR: (1/a^2+bc) + (1/b^2+ac)+ 1/c^2+2ab >=9
Cho a,b>0 TM: a+b<=1 ;CMR: (1/a^b^2)+4b+1/ab>=7
Cho a,b>0 TM:a+b<=1. CMR: 1/1+a^2+b^2 +1/2ab >=8/3
Cho a,b,c>0 TM: a+b+c<=3.CMR: 1/a^2+b^2+c^2 +2009/ab+bc+ac >=670
Cho hình bình hành ABCD , kẻ đường thẳng đi qua A cắt BD ở I, cắt tia BC ở J và cắt tia DC ở K .
a) CMR : AI.ID = IB.IK
b) CMR: IA^2 = IJ.IK
c) CMR: AI/AJ = ID/IB và AI/AK = IB/BD
d) CMR : 1/AJ + 1/AK = 1/AI
CMR: có 1 số gồm toàn CS 1 chia hết cho 19
CMR tồn tại 1 số gồm CS 0 và 1 chia hết cho 2015
CMR: có thể tìm đc 1 STN K sao cho 19K - 1 chi hết cho 10
Chọn dãy
1; 11; 111; ... ;111...1 (số cuối có 20 c/s 1)
Chắc chắn trong dãy có 2 số có cùng số dư khi chia cho 19
2 số đó là
111..1(a c/s 1); 11..1(b c/s 1) [1< a < b < 20]
=>111..1 - 11..1 chia hết cho 19 [b c/s 1 - a c/s 1]
=>111...100...0 chia hết cho 19 [b - a c/s 1 ; a c/s 0]
=>11..1 x 10a chia hết cho 19 [b-a c/s 1]
Mà (19;10)=1 =>(19;10a)=1
=> 111..1 chia hết cho 19 với b-a c/s 1
Đúng 0
Bình luận (0)
Câu 3
Giả Sử: k = 4n
=>194n - 1 = (...1) - 1 = (...0) chia hết cho 10
Vậy có thể tìm đc 1 STN k chia hết cho 10
Đúng 0
Bình luận (0)
xét dãy : 191,192,...,1911
các số tự nhiên khi chia cho 10 có 10 ước là: 0,1,2,..,9
Mà dãy số trên có 11 số nên tồn tại ít nhất 2 số tn có cùng số dư khi chia cho 10
gọi 2 số đó là: 19m và 19n
(11>m>n>1 m,n=1)
19m-19n chia hết cho 10
19n.(19m-n -1) chia hết cho 10
mà (10,19)=1 (19n,10)=1
19m-n-1 chia hết cho 10
19k-1 chia hết cho 10 (k=m-n)
19k-1 chia hết cho 10q
vậy tồn tại 1 số tn k sao cho 19k-1 chia hết cho 10
Đúng 0
Bình luận (0)
Bài 2: Cho tam giác ABC nhọn, đường phân giác AD. Kẻ hình hình hành ABDE.
a. CMR EN.BC=AE.ED
b. CMR: 1/AM=1/AN+1/AC
Điểm N là điểm nào bạn cần ghi chú rõ ra.
Đúng 0
Bình luận (1)
Lời giải:
a. Do $ABDE$ là hbh nên $AE=BD$ và $AE\parallel BD$ nên $AE\parallel DC$
Áp dụng định lý Talet: $\frac{EN}{ND}=\frac{AE}{DC}$
$\Rightarrow \frac{EN}{ED}=\frac{AE}{AE+DC}=\frac{AE}{BD+DC}=\frac{AE}{BC}$
$\Rightarrow EN.BC=AE.ED$ (đpcm)
b.
$\frac{1}{AM}=\frac{1}{AN}+\frac{1}{AC}$
$\Leftrightarrow \frac{AC}{AM}=\frac{AC}{AN}+1(*)$
Thật vậy, áp dụng định lý Talet:
$\frac{AC}{AM}=\frac{AM+MC}{AM}=1+\frac{BC}{AE}=1+\frac{BC}{BD}=1+\frac{BD+DC}{BD}=2+\frac{DC}{BD}(1)$
$\frac{AC}{AN}=\frac{AN+NC}{AN}=1+\frac{NC}{AN}=1+\frac{DC}{AE}=1+\frac{DC}{BD}$
$\Rightarrow \frac{AC}{AN}+1=2+\frac{DC}{BD}(2)$
Từ $(1); (2)\Rightarrow (*)$ đúng, ta có đpcm.
Đúng 1
Bình luận (0)