Cho \(x\) và \(y\) là hai đại lượng tỉ lệ thuận. Khi các giá trị \(x_1,x_2\) của \(x\) có tổng bằng 2 thì hai giá trị tương ứng là \(y_1,y_2\) có tổng bằng -10.
a) Hãy biểu diễn \(y\) theo \(x\)
b) Tính giá trị của \(y\) khi \(x=-1\)
Cho biết x và y là hai đại lượng tỉ lệ thuận, gọi \(x_1;x_2\) là hai giá trị của x và \(y_1;y_2\) là hai giá trị tương ứng của y. Biết \(x_1=6;x_2=-9\) và \(y_1-y_2=10\). Tìm \(y_1;y_2\)
Cho x và y là hai đại lượng tỉ lệ thuận. Khi các giá trị x1, x2 của x có tổng bằng 2 thì hai giá trị tương ứng y1, y2 có tổng bằng -10. Hãy biểu diễn y theo x.
Vì x và y là hai đại lượng tỉ lệ thuận, nên:
y = ax (a là hệ số tỉ lệ, a khác 0)
Khi đó: y1 = a.x1 và y2 = a.x2
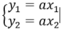
Suy ra y1 + y2 = ax1 + ax2 = a(x1 + x2)
Vậy : y = -5x.
Cho hai đại lượng tỉ lệ nghịch x và y; \(x_1\),\(x_2\) là hai giá trị của x; \(y_1\),\(y_2\) là hai giá trị tương ứng của y. Biết \(x_1\) = 2, \(x_2\)=5 và \(y_1+y_2=21\) khi đó \(y_1\)= ??
A.\(y_1=6\)
B.\(y_1=14\)
C.\(y_1=51\)
D.\(y_1=15\)
Cho x và y là hai đại lượng tỉ lệ thuận. Khi các giá trị x1, x2 của x có tổng bằng 2 thì hai giá trị tương ứng y1, y2 có tổng bằng 10.
a) Hãy biểu diễn y theo x
b) tính giá trị của y khi x = 1
a: x và y là hai đại lượng tỉ lệ thuận
=>\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
mà \(x_1+x_2=2;y_1+y_2=10\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{2}{10}=\dfrac{1}{5}\)
=>\(\dfrac{x}{y}=\dfrac{1}{5}\)
=>y=5x
b: Khi x=1 thì \(y=5\cdot1=5\)
Cho x và y là hai đại lượng tỉ lệ nghịch. Khi x nhận các giá trị \(x_1=2\), \(x_2=5\) thì các giá trị tương ứng của \(y_1\),\(y_2\) thỏa mãn \(3y_1+4y_2=46\). Khi \(x=-10\) thì y=?
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{y_1}{5}=\dfrac{y_2}{2}=\dfrac{3y_1+4y_2}{3\cdot5+4\cdot2}=\dfrac{46}{23}=2\)
Do đó: \(y_1=10;y_2=4\)
\(k=x_1\cdot y_1=10\cdot2=20\)
Khi x=-10 thì y=k/x=20/-10=-2
Cho \(x\) và y là hai đại lượng tỉ lệ nghịch với nhau. Khi \(x\) nhận các giá trị \(x_1=3,x_2=2\) thì các giá trị tương ứng \(y_1,y_2\) có tổng bằng 13
a) Biểu diễn y qua x
b) Tính x khi y = -78
a) Ta co cong thuc:x1/y1=x2/y2
<=>x1.y1=x2.y2
<=>3.y1=2.y2(*)
vi y1+y2=15 nên :
y1=15 - y2
thay vao (*) ta có :3 .(15-y2)=2.y2
<=> 45-3.y2=2.y2<=>
5.y2=45
=>y2=9
=> y1=6
a) Vì x1 và x2 là 2 giá trị tương ứng của x nên
Ta có \(\dfrac{x1}{x2}\)= \(\dfrac{2}{3}\)
=> \(\dfrac{y1}{x2}\)= \(\dfrac{13}{5}.2=\dfrac{26}{5}\)
=> x1.y1=\(\dfrac{26}{5}.3=\dfrac{78}{5}\)
=>y1=\(\dfrac{78}{5.x1}\)
=>y=\(\dfrac{78}{5x}\)
b) Ta có y = \(\dfrac{78}{5}:x\)
Thay y = -78 Ta có
-78 =
Cho x và y là hai đại lượng tỉ lệ thuận; $x_1,x_2$x1,x2 là hai giá trị khác nhau của x và $y_1,y_2$y1,y2 là các giá trị tương ứng của y. Biết $x_1+x_2=5$x1+x2=5 và $y_1+y_2=20$y1+y2=20. Hãy tìm hệ số tỉ lệ của y đối với x?
Giả sử x và y là hai đại lượng tỉ lệ thuận, \(x_1\)\(x_2\)là 2 giá trị khác nhau của x và \(y_1\);\(y_2\)là 2 giá trị tương ứng của y. Tính \(y_1\)bt: \(x_1\)= 12; \(x_2\)= \(\dfrac{1}{6}\) ; \(y_2=\dfrac{1}{3}\)
Vì x,y tỉ lệ thuận nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{1}{6}:\dfrac{1}{3}=\dfrac{1}{2}\)
\(\Rightarrow y_1=2x_1=24\)