Cho hình lập phương ABCD,A'B'C'D'. Biết AC =4\(\sqrt{2}\) tính S\(_{xq}\), S\(_{tp}\) và thể tích hình lập phương
Những câu hỏi liên quan
1. Một hình hộp chữ nhật có chiều dài là 1,3cm , chiều rộng là 1,2cm và chiều cao là 1,8m . Tính S xq và S tp của hình hộp đó .
2. Một cái hộp hình lập phương có cạnh là 1,6dm . Tính S xq và S tp của hình lập phương đó .
Bài 1:
Đổi 1,8m = 0,018cm
Diện tích xung quanh là : ( 1,3 + 1,2 ) x 2 x 0,018 = 0,09 ( cm2 )
Diện tích toàn phần là : 0,09 + 1,3 x 1,2 x 2 = 3, 21 ( cm2 )
Đ/s : 0,09 cm2 ; 3,21 cm2
Bài 2 :
Diện tích xung quanh là :
( 1,6 x 1,6 ) x 4 = 10,24 ( dm2 )
Diện tích toàn phần là : ( 1,6 x 1,6 ) x 6 = 15 , 36 ( dm2 )
Đ/s 10,24 dm2 ; 15,36 dm2
Đúng 0
Bình luận (0)
1. Đổi: 1,8m = 180 cm
Diện tích xung quanh của hình hộp chữ nhật đó là:
\(S_{xq}=2\times h\times\left(a+b\right)=2\times180\times\left(1,3+1,2\right)=900\left(cm^2\right)\)
Diện tích toàn phần của hình hình hộp chữ nhật đó là:
\(S_{tp}=S_{xq}+2\times a\times b=900+2\times1,3\times1,2=903,12\left(cm^2\right)\)
2. Diện tích xung quanh của hình lập phương đó là:
\(S_{xq}=4\times a^2=4\times1,6^2=10,24\left(dm^2\right)\)
Diện tích toàn phần của hình lập phương đó là:
\(S_{tp}=6\times a^2=6\times1,6^2=15,36\left(dm^2\right)\)
Đáp số: .....
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hình vuông ABCD và ABCD. Tính S. A.
S
πa
2
B.
S
πa
2
2
2
C.
S
πa
2
2
D.
S...
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hình vuông ABCD và A'B'C'D'. Tính S.
A. S = πa 2
B. S = πa 2 2 2
C. S = πa 2 2
D. S = πa 2 3
Đáp án C
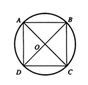
Do hình trụ và hình lập phương có cùng chiều cao nên ta chỉ cần chú ý đến mặt đáy như hình vẽ bên. Đường tròn đáy của hình trụ có bán kính bằng một nửa đường chéo của hình vuông ABCD; R = a 2 2
Do đó thể tích hình trụ cần tìm bằng S = 2 πRh = 2 π a 2 2 a = πa 2 2 .
Đúng 0
Bình luận (0)
1. Cho hình lập phương ABCD. A'B'C'D'. Xác định góc giữa 2 đg thẳng AC VÀ BC'. 2. Cho tứ diện đều ABCD góc giữa 2 vecto AB ,CD có số đo là? 3. Cho hình lập phương ABCD. A'B'C'D' có M,N lần lượt thuộc 2 cạnh AA' và DD' sao cho AN= NA' ; DD'=4DM . Tính cosa vs a= ( MN,B'D')
Cho hình lập phương ABCD.ABCD có cạnh bằng 2a Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và ABCD Diện tích S là
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 2a Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A'B'C'D' Diện tích S là
Cho hình lập phương
A
B
C
D
.
A
B
C
D
có cạnh bằng 2a Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và
A
B
C
D
.
Diện tích S là A.
4
π
a
2
2
B. ...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng 2a Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD và A ' B ' C ' D ' . Diện tích S là
A. 4 π a 2 2
B. π a 2 2
C. π a 2 3
D. π a 2
Đáp án A
Bán kính đáy là R = a 2
Diện tích xung quanh hình trụ là S x q = 2 π R l = 2 π . a 2 .2 a = 4 π a 2 2
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD. ABCD, gọi M và N lần lượt là tâm của các hình vuông ABCD và DCCD. Mặt phẳng (AMN) chia khối lập phương trình hai phần có thể tích là V₁ và V₂ (V₁ V₂). Tính tỷ số V₂/V₁ A. 5/2 B. 5/3 C. 3/2 D. 2
Đọc tiếp
Cho hình lập phương ABCD. A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và DCC'D'. Mặt phẳng (A'MN) chia khối lập phương trình hai phần có thể tích là V₁ và V₂ (V₁ < V₂). Tính tỷ số V₂/V₁
A. 5/2
B. 5/3
C. 3/2
D. 2
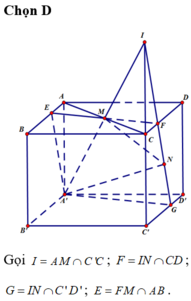
Vậy thiết diện của hình hộp cắt bởi mặt phẳng (A'MN) là hình bình hành A'EFG.
Ta có:
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.ABCD, gọi M và N lần lượt là tâm của các hình vuông ABCD và ABCD. Mặt phẳng (AMN) chia khối lập phương thành hai phần có thể tích là
V
1
và
V
2
. Tính tỷ số
V
2
V
1
.
Đọc tiếp
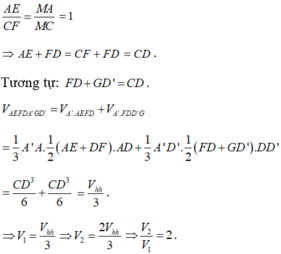
Cho hình lập phương ABCD.A'B'C'D', gọi M và N lần lượt là tâm của các hình vuông ABCD và A'B'C'D'. Mặt phẳng (A'MN) chia khối lập phương thành hai phần có thể tích là V 1 và V 2 . Tính tỷ số V 2 V 1 .
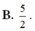
Tính thể tích hình lập phương biết: a. Stp là 0,54m3; b. S xq là 36 dm3.
a: Độ dài cạnh là:
\(\sqrt{0.54:6}=0.3\left(m\right)\)
Thể tích là \(0.3^3=0.027\left(m^3\right)\)
b: Độ dài cạnh là:
\(\sqrt{\dfrac{36}{4}}=3\left(dm\right)\)
Thể tích là \(3^3=27\left(dm^3\right)\)
Đúng 0
Bình luận (0)
Cho hình lập phương ABCD.
A
B
C
D
; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện
O
A
B
C
bằng A.
a
3
12
B.
a
3
24
C.
a
3...
Đọc tiếp
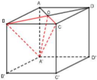
Cho hình lập phương ABCD. A ' B ' C ' D ; cạnh bằng a. Gọi O là giao điểm của AC và BD. Thể tích của tứ diện O A ' B C bằng
A. a 3 12
B. a 3 24
C. a 3 6
D. a 3 4
