Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số \(\dfrac{1}{2}\)

Những câu hỏi liên quan
Cho tam giác \(ABC\), hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng \(k = \frac{1}{2}\).
Bước 1: Vẽ tam giác \(ABC\) bất kì.
Bước 2: Gọi \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\).
Khi đó ta có \(\Delta AMN\backsim\Delta ABC\) theo tỉ số \(k = \frac{1}{2}\).
Chứng minh:
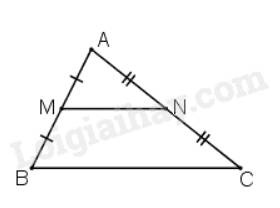
Vì \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\)\( \Rightarrow \left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right.\).
Ta có \(MN//BC\) và \(M,N\) cắt \(AB,AC\) tại \(M,N\) nên \(\Delta AMN\backsim\Delta ABC\) (định lí).
Khi đó, \(\frac{{MN}}{{BC}} = \frac{1}{2}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số 1/2.
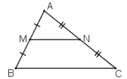
Gọi M là trung điểm AB, N là trung điểm AC.
⇒ MN là đường trung bình của tam giác ABC
⇒ MN // BC
⇒ ΔAMN 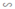 ΔABC theo tỉ số
ΔABC theo tỉ số 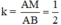
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số 1/2.
Cho trước tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số \(k=\dfrac{2}{3}\)
cho tam giác ABC. hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số \(\frac{1}{2}\)
Đặt M là trung điểm của AB và N là trung điểm của AC. Vẽ MN song song với BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC. Hãy dựng một tam giác đồng dạng với tam giác ABC theo tỉ số k =2/3
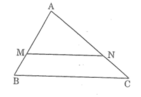
* Cách dựng:
- Trên cạnh AB dựng điểm M sao cho AM = 2/3 AB
- Trên cạnh AC dựng điểm N sao cho AN = 2/3 AC
- Dựng đoạn thẳng MN ta được tam giác AMN đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3
* Chứng minh:
Theo cách dựng ta có:
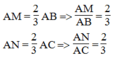
Suy ra: 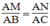
Trong ΔABC, ta có: 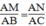
Theo định lí đảo của định lí Ta-lét ta có: MN // BC
Vậy
△
AMN đồng dạng
△
ABC và 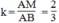
Đúng 0
Bình luận (0)
Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ lệ đồng dạng \(k=\dfrac{2}{3}\)
Giải:
Trên cạnh AB lấy điểm M sao cho AM= AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)
Đúng 0
Bình luận (0)
Trên cạnh AB lấy điểm M sao cho AM= 232323AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=232323
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)
Đúng 0
Bình luận (0)
Trên cạnh AB lấy điểm M sao cho AM= \(\dfrac{2}{3}\)AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=\(\dfrac{2}{3}\)
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc đồng dạng với tam giác khg theo tỉ số 2:3 và tam giác khg đồng dạng với tam giác mnp theo tỉ số 1:3 vậy tam giác abc đồng dạng với tam giác mnp theo tỉ số nào
ΔABC~ΔKHG
=>\(\dfrac{AB}{KH}=\dfrac{2}{3}\)
=>\(KH=AB\cdot\dfrac{3}{2}\)
ΔKHG~ΔMNP
=>\(\dfrac{KH}{MN}=\dfrac{1}{3}\)
=>\(\dfrac{AB}{MN}\cdot\dfrac{3}{2}=\dfrac{1}{3}\)
=>\(\dfrac{AB}{MN}=\dfrac{1}{3}:\dfrac{3}{2}=\dfrac{2}{9}\)
=>ΔABC đồng dạng với ΔMNP theo tỉ số \(\dfrac{2}{9}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3.
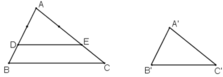
+ Dựng ΔADE  ΔABC theo tỉ số 2/3
ΔABC theo tỉ số 2/3
Trên AB lấy D, trên AC lấy E sao cho 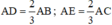
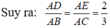
Khi đó theo định lý Ta-let đảo ta suy ra DE // BC
⇒ ΔADE 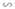 ΔABC theo tỉ số 2/3.
ΔABC theo tỉ số 2/3.
+ Dựng ΔA’B’C’ = ΔADE
Vẽ đoạn A’B’ = AD.
Dựng góc 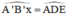
Trên tia B’x lấy điểm C’ sao cho B’C’ = DE.
Nối C’A’ ta được ΔA’B’C’ = ΔADE (c.g.c)
Suy ra: ΔA’B’C’ đồng dạng với ΔADE theo tỉ số:
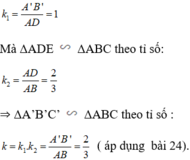
Đúng 0
Bình luận (0)




















