Chứng minh định lý: Trong 1 tam giác cân, 2 đường trung tuyến ứng với 2 cạnh bên thì bằng nhau

Những câu hỏi liên quan
1. Hãy chứng minh định lý: trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
2. Hãy chứng minh định lí: nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân.
Giúp mình với!
Ai nhanh 3 tick
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)
Đúng 0
Bình luận (0)
chứng minh định lý : trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau
giúp mik làm bài này nha !
Bạn vẽ hình ra và gọi hai cạnh bên của tam giác cân đó lần lượt là AB, AC.
Gọi E, F lần lượt là trung điểm của các cạnh AB, AC.
Nối E, F với các đỉnh đối diện các cạnh AB, AC ta được 2 tam giac ABF, ACE
Ta có 2 tam giác trên bằng nhau theo trường hợp c.g.c
AB = AC
(Cạnh bên của tam giác cân)
Góc A chung AE = AF => cạnh BF = CE (là 2 đường trung tuyến ứng vói 2 cạnh bên của tam giác cân)
=>Đpcm
Đúng 0
Bình luận (0)
Chứng minh định lí: trong một tam giác cân , hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.?
Và
Hãy chứng minh định lí đảo của định lí trên: nếu hai tam giác có hai đường trung tuyến bằng nhau thì tam giác đó là tam giác cân
Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Giả sử ΔABC cân tại A có hai đường trung tuyến BM và CN, ta cần chứng minh BM = CN.
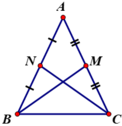
Ta có: AC = 2.AM, AB = 2. AN, AB = AC (vì ΔABC cân tại A)
⇒ AM = AN.
Xét ΔABM và ΔACN có:
AM = AN
AB = AC
Góc A chung
⇒ ΔABM = ΔACN (c.g.c) ⇒ BM = CN (hai cạnh tương ứng).
(Còn một số cách chứng minh khác, nhưng do giới hạn kiến thức lớp 7 nên mình xin sẽ không trình bày.)
Đúng 0
Bình luận (0)
CHỨNG MINH ĐỊNH LÍ : TRONG MỘT TAM GIÁC CÂN, HAI ĐƯỜNG TRUNG TUYẾN ỨNG VỚI HAI CẠNH BÊN THÌ BẰNG NHAU
Chứng minh rằng:
a) Trong một tam giác cân, hai đường trung tuyến ứng với 2 cạnh bên là hai đoạn thẳng bằng nhau.
b) Ngược lại, nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Gọi BM, CN là 2 đường trung tuyến của \(\Delta ABC\)
\( \Rightarrow \)MA = MC = \(\dfrac{1}{2}\)AC; NA = NB = \(\dfrac{1}{2}\)AB
Vì \(\Delta ABC\) cân tại A nên AB = AC ( tính chất)
Do đó, AM = MC = NA = NB
Xét \(\Delta \)ANC và \(\Delta \)AMB, ta có:
AN = AM
\(\widehat A\) chung
AC = AB
\( \Rightarrow \)\(\Delta \)ANC = \(\Delta \)AMB (c.g.c)
\( \Rightarrow \) NC = MB ( 2 cạnh tương ứng)
Vậy 2 đường trung tuyến ứng với 2 cạnh bên của tam giác cân là hai đoạn thẳng bằng nhau.

Vì \(∆ABC\) có hai đường trung tuyến \(BM\) và \(CN\) cắt nhau ở \(G\)
\(\Rightarrow \) \(G\) là trọng tâm của tam giác \(ABC\).
\(\Rightarrow GB = \dfrac{2}{3}BM\); \(GC = \dfrac{2}{3}CN\) ( tính chất đường trung tuyến trong tam giác)
Mà \(BM = CN\) (giả thiết) nên \(GB = GC.\)
Tam giác \(GBC\) có \(GB = GC\) nên \(∆GBC\) cân tại \(G\).
\(\Rightarrow \) \(\widehat{GCB} = \widehat{GBC}\) (Tính chất tam giác cân).
Xét \(∆BCN\) và \(∆CBM\) có:
+) \(BC\) là cạnh chung
+) \(CN = BM\) (giả thiết)
+) \(\widehat{GCB} = \widehat{GBC}\) (chứng minh trên)
Suy ra \(∆BCN = ∆CBM\) (c.g.c)
\(\Rightarrow \) \(\widehat{NBC} = \widehat{MCB}\) (hai góc tương ứng).
\(\Rightarrow ∆ABC\) cân tại \(A\) (tam giác có hai góc bằng nhau là tam giác cân)
Đúng 0
Bình luận (0)
Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN (đpcm)
Đúng 0
Bình luận (0)
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
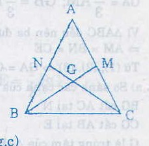
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN
Đúng 0
Bình luận (0)
Chứng minh định lí: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
Ta có AN = NB = AB/2 (Tính chất đường trung tuyến)
AM = MC = AC/2 (Tính chất đường trung tuyến)
Vì ∆ ABC cân tại A=> AB = AC nên AM = AN
Xét ∆BAM ;∆CAN có:
AM = AN (cm trên)
Góc A chung
AB = AC (∆ABC cân)
Nên suy ra ∆BAM = ∆CAN (c-g-c)
=> BM = CN ( 2 cạnh tương ứng)
Đúng 0
Bình luận (1)
Chứng minh định lí : Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau ?
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
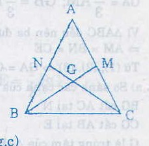
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN
Đúng 0
Bình luận (0)
Chứng minh định lí : Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.
tick mk di bao gio mk hoc roi thi mk giai cho
Đúng 0
Bình luận (0)
nếu trong định lí ghi vậy thì chắc chắn điều này luồn đúng, đéo cần chứng minh cũng biết
Đúng 0
Bình luận (0)
Su dung cac tinhchat tam giac can ma cm 2 tam giac bang nhau
Duong trung tuyen la dg trung trc,,Duong cao ,,,,ra dc ma
Tick mik nke
Đúng 0
Bình luận (0)

























