Nêu quy tắc biểu diễn hình học tập nghiệm của bất phương trình \(ax+by\le c\)

Những câu hỏi liên quan
Nếu quy tắc biểu diễn hình học tập nghiệm của bất phương trình ax + by ≤ c.
- Vẽ đường thẳng (d): ax + by = c.
- Chọn điểm M(xo, yo) không thuộc (d) (thường chọn điểm (0; 0)) và tính giá trị axo + byo.
- So sánh axo + byo với c:
+ Nếu axo + byo < c thì tọa độ điểm M thỏa mãn bất phương trình nên miền nghiệm là nửa mặt phẳng bờ (d) (tính cả đường thẳng d) chứa điểm M
+ Nếu axo + byo > c thì tọa độ điểm M không thỏa mãn bất phương trình nên miền nghiệm là nửa mặt phẳng bờ (d) (tính cả đường thẳng d) không chứa điểm M.
Đúng 0
Bình luận (0)
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:
\(\left\{ \begin{array}{l}x - 2y + 3 \le 0\\x + 3y > - 2\\x \le 0\end{array} \right.\)
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau.
Bước 1: Mở trang Geoebra
Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).
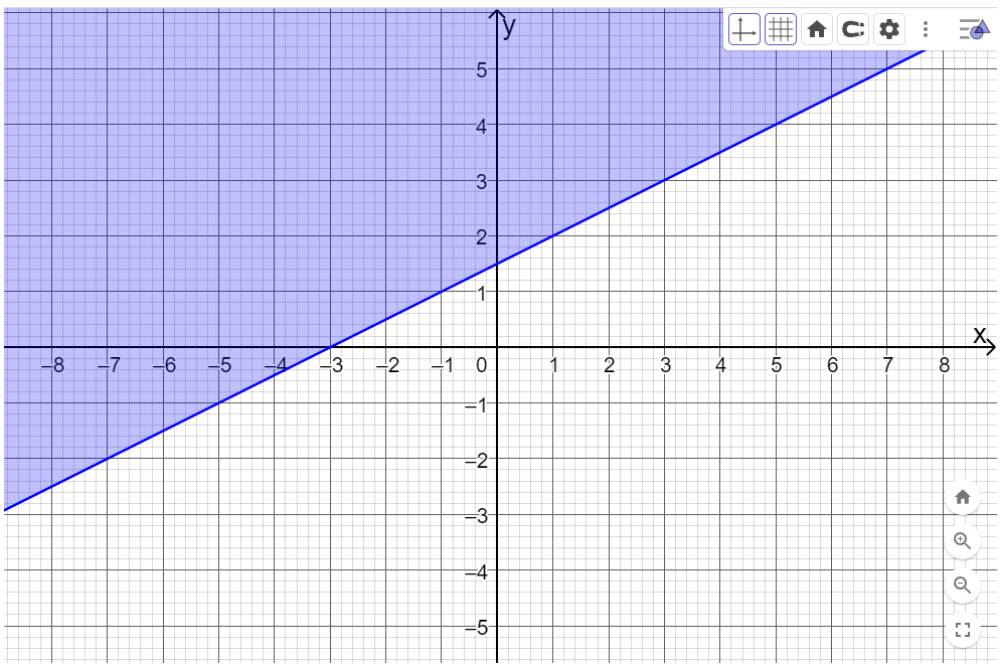
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:
x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.
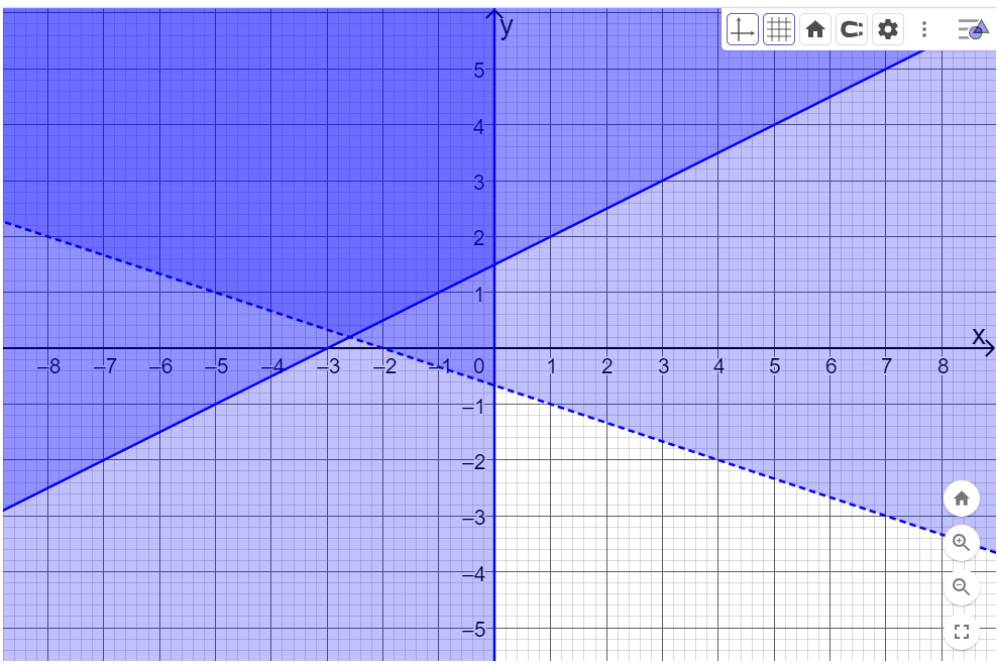
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y = - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.
Đúng 0
Bình luận (0)
Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).
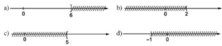
a) Hình a biểu diễn tập nghiệm của bất phương trình x ≤ 6
b) Hình b biểu diễn tập nghiệm của bất phương trình x > 2
c) Hình c biểu diễn tập nghiệm của bất phương trình x ≥ 5
d) Hình d biểu diễn tập nghiệm của bất phương trình x < -1
Đúng 0
Bình luận (0)
Nêu quy tắc giải bất phương trình ax +by = <_c
biểu diễn hình học tập nghiệm của bất phương trình x-2y>1
x-2y>1
=>-2y>1-x
=>2y<x-1
=>\(y< \dfrac{1}{2}x-\dfrac{1}{2}\)
Trên đường y=1/2x-1/2, ta thấy O(0;0) không thuộc \(y=\dfrac{1}{2}x-\dfrac{1}{2}\)
Thay x=0 vào 1/2x-1/2, ta được:
\(\dfrac{1}{2}\cdot0-\dfrac{1}{2}=-\dfrac{1}{2}< 0\)
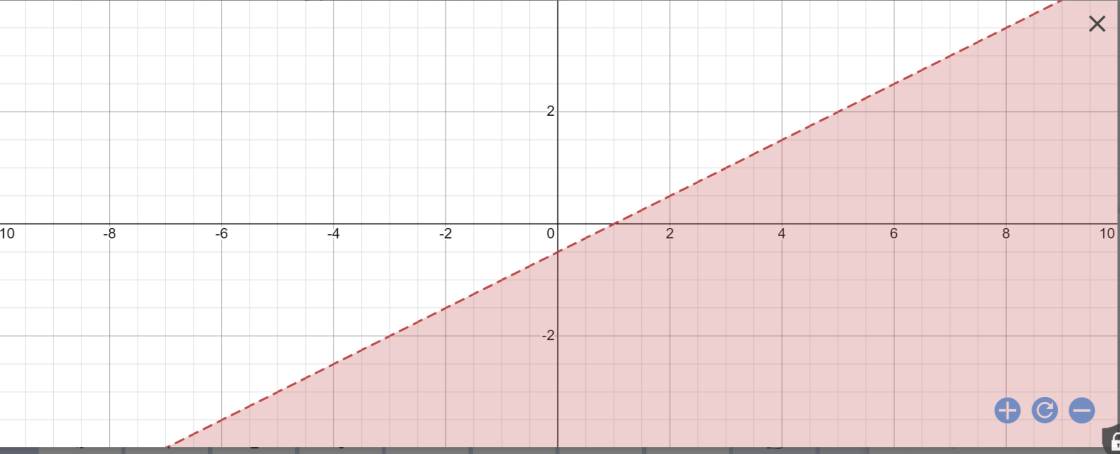
Do đó, tập nghiệm của BPT x-2y>1 sẽ là nửa mặt phẳng không chứa biênvà cũng không chứa điểm 0 của đường thẳng x-2y=1
=>
Đúng 0
Bình luận (0)
Biểu diễn hình học tập nghiệm của các bất phương trình sau: 2x - 1 < 0
Miền nghiệm là nửa mặt phẳng bờ 2x – 1 = 0 chứa O (bỏ bờ).
Đúng 0
Bình luận (0)
Biểu diễn hình học tập nghiệm của các bất phương trình sau: 2x + y > 1
Miền nghiệm là nửa mặt phẳng bờ 2x + y = 1 không chứa O (bỏ bờ).
Đúng 0
Bình luận (0)
Biểu diễn hình học tập nghiệm của các bất phương trình sau: 3 + 2y > 0
Điểm O(0;0) có tọa độ thỏa mãn bất phương trình, do đó miền nghiệm là nửa mặt phẳng bờ 3 + 2y = 0 chứa O (bỏ bờ).
Đúng 0
Bình luận (0)
Biểu diễn hình học tập nghiệm của các bất phương trình sau: x - 5y < 2
Miền nghiệm là nửa mặt phẳng bờ -x + 5y = -2 chứa O (bỏ bờ)
Đúng 0
Bình luận (0)









