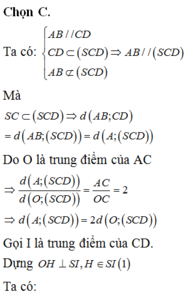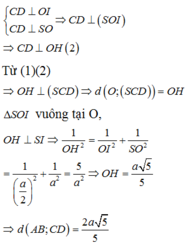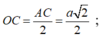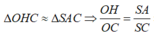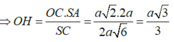cho hình vuông abcd cạnh a ,tâm o ;sa\(\perp\)(abcd) . Tính sa theo a để số đo của góc giữa 2mp (scb) và (scd) bằng 60o

Những câu hỏi liên quan
Cho hình vuông ABCD cạnh a, tâm O. Tính
O
B
→
+
O
C
→
Đọc tiếp
Cho hình vuông ABCD cạnh a, tâm O. Tính O B → + O C →
![]()
![]()
![]()
![]()
Chọn A.

Gọi M là trung điểm của BC.
![]() = 2OM = AB = a.
= 2OM = AB = a.
Đúng 0
Bình luận (0)
Cho hình vuông ABCD cạnh a, tâm O. Tính
O
B
→
+
O
C
→
A.
O
B
→
+
O
C...
Đọc tiếp
Cho hình vuông ABCD cạnh a, tâm O. Tính O B → + O C →
A. O B → + O C → = a .
B. O B → + O C → = a 2 .
C. O B → + O C → = a 2 .
D. O B → + O C → = a 2 2 .

Gọi M là trung điểm của BC.
Tam giác ABC có O ; M lần lượt là trung điểm của AC ; BC nên OM là đường trung bình của
tam giác
Suy ra : AB = 2OM.
Ta có O B → + O C → = 2 O M → = 2 O M = A B = a .
Đáp án A
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD, SA vuông góc (ABCD), SC = √3 . ABCD là hình vuông cạnh a, tâm O. G là trọng tâm tam giác SCD. Tính khoảng cách giữa OG và AD
Cho hình vuông ABCD và hình tròn tâm O như hình vẽ. Biết cạnh của hình vuông bằng 5cm. a) Tính bán kính hình tròn tâm O. b) Tính diện tích phần gạch chéo.
a) Để tính bán kính hình tròn tâm O, ta có thể sử dụng định lý Pytago trong tam giác vuông AOB:
AB^2 + OB^2 = AO^2
Vì AB là cạnh của hình vuông và bằng 5cm, nên AB^2 = 5^2 = 25cm^2.
Vì O là tâm của hình tròn, nên OB là bán kính của hình tròn.
Vậy, ta có: 25 + OB^2 = AO^2
Vì tam giác AOB là tam giác vuông, nên ta có thể sử dụng định lý Pytago trong tam giác vuông AOC:
AC^2 = AO^2 + OC^2
Vì AC là đường chéo của hình vuông và bằng cạnh hình vuông nhân căn 2, nên AC = 5√2 cm.
Vì OC là bán kính của hình tròn, nên ta có: AC^2 = AO^2 + OC^2
Kết hợp hai phương trình trên, ta có hệ phương trình:
25 + OB^2 = AO^2
AC^2 = AO^2 + OC^2
Thay giá trị vào, ta có:
25 + OB^2 = AO^2
(5√2)^2 = AO^2 + OC^2
50 = AO^2 + OC^2
Do đó, ta có thể giải hệ phương trình để tính được giá trị của OB (bán kính hình tròn) và OC (đường cao của tam giác vuông AOC).
b) Để tính diện tích phần gạch chéo, ta cần biết độ dài của đường chéo và biết rằng đường chéo chia hình vuông thành hai tam giác vuông cân. Vì đường chéo là cạnh của hình vuông, nên độ dài đường chéo là 5cm.
Diện tích phần gạch chéo sẽ bằng tổng diện tích hai tam giác vuông cân. Với cạnh của hình vuông là 5cm, ta có thể tính diện tích một tam giác vuông cân bằng công thức: diện tích = (cạnh)^2 / 2.
Vậy diện tích phần gạch chéo sẽ là: 2 * [(5^2) / 2] = 25 cm^2.
15:31
Đúng 1
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a , SA vuông góc ABCD , SA =a√2
a) CM : BD vuông góc SAC
b) tính góc giữa SC và mp ABCD
25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
Đúng 0
Bình luận (0)
26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)
Đúng 0
Bình luận (0)
27.
a.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông ABCD cạnh a, gọi O là tâm đường tròn nội tiếp hình vuông. Tìm khẳng định đúng?
A. AB, BC, CD và DA là các tiếp tuyến của đường tròn (O).
B. AB, BC, CD và DA đều không là tiếp tuyến của đường tròn (O).
C. AC và BD là tiếp tuyến của (O).
D. Tất cả sai.
Đáp án A
Gọi O là giao điểm của AC và BD. Khi đó, đường tròn tâm O bán kính R = a/2 là đường tròn nội tiếp hình vuông ABCD.
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên đường tròn tiếp xúc với các cạnh của hình vuông.
Suy ra: AB; BC; CD và DA là các tiếp tuyến của đường tròn (O).
Đúng 0
Bình luận (0)
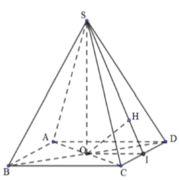
Cho hình chóp .S ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và
S
O
a
. Khoảng cách giữa SC và AB bằng
Đọc tiếp
Cho hình chóp .S ABCD có đáy ABCD là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng (ABCD) và S O = a . Khoảng cách giữa SC và AB bằng
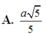
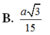
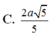
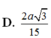
Cho hình chóp S.ABCD có SA ⊥ (ABCD), SA 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC. A.
a
3
3
B.
a
3
4
C.
a
2
3
D.
a
2...
Đọc tiếp
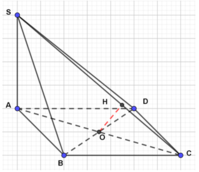
Cho hình chóp S.ABCD có SA ⊥ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
A. a 3 3
B. a 3 4
C. a 2 3
D. a 2 4
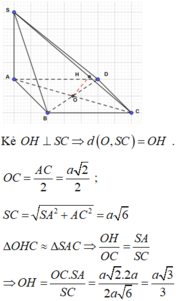
Chọn A.
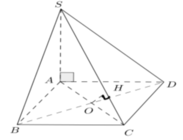
- Kẻ )H ⊥ SC, khi đó d(O; SC) = OH.
- Ta có: ΔSAC ~ ΔOHC (g-g) nên:
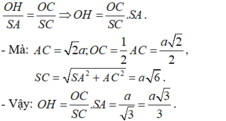
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có
S
A
⊥
A
B
C
D
, SA2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC A.
a
2
4
B.
a
3
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có S A ⊥ A B C D , SA=2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC
A. a 2 4
B. a 3 3
C. a 3 4
D. a 2 3
Cho hình chóp S.ABCD có SA
⊥
(ABCD),SA2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC. A.
a
2
4
B.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABCD có SA ⊥ (ABCD),SA=2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
A. a 2 4
B. a 3 3
C. a 3 4
D. a 2 3