Gọi M là trung điểm của BC.
Tam giác ABC có O ; M lần lượt là trung điểm của AC ; BC nên OM là đường trung bình của
tam giác
Suy ra : AB = 2OM.
Ta có O B → + O C → = 2 O M → = 2 O M = A B = a .
Đáp án A
1. Cho đường tròn (O). Trên đường tròn đó lấy ngẫu nhiên 3 điểm A, B, C. Tính xác suất để \(\Delta ABC\) chứa tâm O của đường tròn.
2. Cho hình cầu tâm (O). Trên mặt hình cầu lấy ngẫu nhiên 4 điểm A, B, C, D. Tính xác suất để hình tứ diện ABCD chứa tâm O của hình cầu.
Cho lục giác đều $A B C D E F$ tâm $O$. Chứng minh: $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}+\overrightarrow{O D}+\overrightarrow{O E}+\overrightarrow{O F}=\overrightarrow{0}$.
1)Cho hình bình hành ABCD, xác định các vectơ DA+DC,AB+DA.
2)Cho 5 điểm A, B, C, D, E. Chứng minh rằng: AC-ED+CD+EC-BC = AB
3)Cho hình vuông ABCD, tâm O cạnh bằng a.
a) Xác định vecto BA+DA+AC, AB+CA+BC, AB+AC.
b) Tính độ dài vecto DA+DC, AB-BC
Cho hình vuông ABCD có cạnh a, O là giao điểm 2 đườg chéo . a) tính |vectoOA - vectoOC| b) tính | vectoAB - vectoCD|
Cho hình vuông ABCD cạnh a, tâm O. Tính O B → + O C →
Cho hình bình hành ABCD có B A D ^ < 90 ∘ . Giả sử O là điểm nằm trong Δ A B D sao cho OC không vuông góc với BD.
Vẽ đường tròn tâm O đi qua C. BD cắt (O) tại hai điểm M, N sao cho B nằm giữa M, D.
Tiếp tuyến tại C của (O) cắt AD, AB lần lượt tại P, Q
1) Chứng minh rằng bốn điểm M, N, P, Q cùng thuộc một đường tròn.
1. Cho hình vuông ABCD cạnh a. Tính độ dài vectơ v= vectơ AC+ vectơ BD
2. Cho hình vuông tâm O cạnh a. Tính độ dài vectơ v= vectơ OA+ vectơ DC
Trong mặt phẳng tọa độ Oxy. Cho hình thoi ABCD cạnh a và B A D ^ = 60 ° . Biết A trùng với gốc tọa độ O; C thuộc trục Ox và xB; yB ≥ 0. Tìm tọa độ các đỉnh B và C của hình thoi ABCD.
A.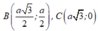 
B.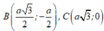 
C.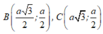 
D. 
