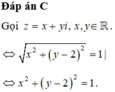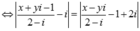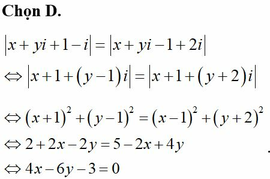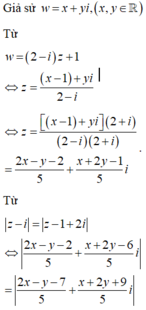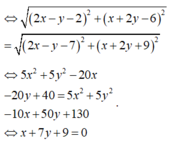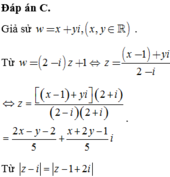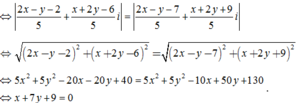Giải phương trình số phức sau:
|z| + z = 2+2i

Những câu hỏi liên quan
Giải các phương trình sau trên tập số phức:
(3 + 2i)z - (4 + 7i) = 2 - 5i
(3 + 2i).z - (4 + 7i) = 2 – 5i
⇔ (3 + 2i).z = (2 – 5i) + (4 + 7i)
⇔ (3 + 2i).z = 6 + 2i
Đúng 0
Bình luận (0)
Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn
z
−
2
i
1
là đường tròn có phương trình nào sau đây? A.
x
−
2
2
+
y
2
0
B.
x...
Đọc tiếp
Tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn z − 2 i = 1 là đường tròn có phương trình nào sau đây?
A. x − 2 2 + y 2 = 0
B. x 2 + y − 2 2 = 0
C. x 2 + y − 2 2 = 1
D. x − 2 2 + y 2 = 1
Tìm số phức z thỏa mãn hệ phương trình:
z
-
2
i
z
z
-
i...
Đọc tiếp
Tìm số phức z thỏa mãn hệ phương trình:
z - 2 i = z z - i = z - 1
Đặt z = x + yi , ta được hệ phương trình:
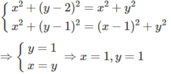
Vậy z = 1 + i.
Đúng 0
Bình luận (0)
Cho số phức thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp điểm biểu diễn số phức w (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
Đọc tiếp
Cho số phức thỏa mãn z - i = z - 1 + 2 i . Tập hợp điểm biểu diễn số phức w = (2 - i) z +1 trên mặt phẳng phức là một đường thẳng. Phương trình của đường thẳng đó là
![]()
![]()
![]()
![]()
Kí hiệu
z
1
,
z
2
là hai nghiệm phức của phương trình
z
2
+
2
i
Gọi M,N là các điểm biểu diễn của các số phức
z
1
,
z
2
Tính
z
2...
Đọc tiếp
Kí hiệu z 1 , z 2 là hai nghiệm phức của phương trình z = 2 + 2 i Gọi M,N là các điểm biểu diễn của các số phức z 1 , z 2 Tính z = 2 + 2 i với O là gốc toạ độ.
A. T = 2 2 .
B. T = 2 2
C. T = 2 2 .
D. T = 2 2
Cho số phức z thỏa:
2
z
-
2
+
3
i
2
i
-
1
-
2
z
. Tập hợp điểm biểu diễn cho số phức z là một đường thẳng có phương trình là: A. 20x-16y-470 B. 20x+16y+470 C. 20x+32y-470 D. -20x+32y+470
Đọc tiếp
Cho số phức z thỏa: 2 z - 2 + 3 i = 2 i - 1 - 2 z . Tập hợp điểm biểu diễn cho số phức z là một đường thẳng có phương trình là:
A. 20x-16y-47=0
B. 20x+16y+47=0
C. 20x+32y-47=0
D. -20x+32y+47=0
Cho các số phức z thỏa mãn
z
+
1
-
i
z
-
1
+
2
i
. Tập hợp các điểm biểu diễn số phức z là một đường thẳng. Viết phương trình đường thẳng đó A. 4x+6y-30 B. 4x+6y+30 C. 4x-6y+30 D. 4x-6y-30
Đọc tiếp
Cho các số phức z thỏa mãn z + 1 - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức z là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3=0
B. 4x+6y+3=0
C. 4x-6y+3=0
D. 4x-6y-3=0
Cho các số phức z thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
(
2
-
i
)
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A.
x
-
7
y
-
9
0...
Đọc tiếp
Cho các số phức z thỏa mãn z - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = ( 2 - i ) z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x - 7 y - 9 = 0
B. x + 7 y - 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Cho các số phức z thỏa mãn
z
−
i
z
−
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
2
−
i
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A....
Đọc tiếp
Cho các số phức z thỏa mãn z − i = z − 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = 2 − i z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x − 7 y − 9 = 0
B. x + 7 y − 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0