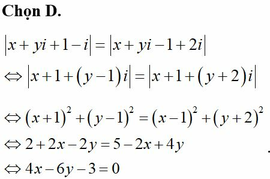Các câu hỏi tương tự
Cho các số phức z thỏa mãn |z+1-i|=|z-1+2i|. Tập hợp các điểm biểu diễn các số phức z trên mặt phẳng tọa độ là một đường thẳng. Viết phương trình đường thẳng đó
A. 4x+6y-3= 0
B. 4x-6y-3=0
C. 4x+6y+3=0
D. 4x-6y+3=0
Cho các số phức z thỏa mãn
z
-
i
z
-
1
+
2
i
. Tập hợp các điểm biểu diễn số phức
w
(
2
-
i
)
z
+
1
trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là A.
x
-
7
y
-
9
0...
Đọc tiếp
Cho các số phức z thỏa mãn z - i = z - 1 + 2 i . Tập hợp các điểm biểu diễn số phức w = ( 2 - i ) z + 1 trên mặt phẳng tọa độ là một đường thẳng. Phương trình đường thẳng đó là
A. x - 7 y - 9 = 0
B. x + 7 y - 9 = 0
C. x + 7 y + 9 = 0
D. x - 7 y + 9 = 0
Cho số phức z thay đổi hoàn toàn thỏa mãn:
z
−
i
z
−
1
+
2
i
. Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn:
w
2
−...
Đọc tiếp
Cho số phức z thay đổi hoàn toàn thỏa mãn: z − i = z − 1 + 2 i . Tập hợp các điểm trên mặt phẳng tọa độ biểu diễn số phức w thỏa mãn: w = 2 − i z + 1 là một đường thẳng. Viết phương trình đường thẳng đó.
A. − x + 7 y + 9 = 0.
B. x + 7 y − 9 = 0.
C. x + 7 y + 9 = 0.
D. x − 7 y + 9 = 0.
Tập hợp các điểm biểu diễn số phức z thỏa mãn là đường thẳng
z
-
1
+
i
z
+
1
-
2
i
là đường thẳng
∆
:
a
x
+
b
y
+
c
0
. Tính ab + c A. 15 B...
Đọc tiếp
Tập hợp các điểm biểu diễn số phức z thỏa mãn là đường thẳng z - 1 + i = z + 1 - 2 i là đường thẳng ∆ : a x + b y + c = 0 . Tính ab + c
A. 15
B. 9
C. 11
D. 6
Tập hợp các điểm trong mặt phức biểu diễn số phức z thỏa mãn
2
i
z
−
1
2
z
+
3
là một đường thẳng có phương trình A.
24
x
+
4
y
+
35
0.
B.
24
x
−
4
y
−
3...
Đọc tiếp
Tập hợp các điểm trong mặt phức biểu diễn số phức z thỏa mãn 2 i z − 1 = 2 z + 3 là một đường thẳng có phương trình
A. 24 x + 4 y + 35 = 0.
B. 24 x − 4 y − 35 = 0.
C. 24 x + 4 y − 35 = 0.
D. 24 x − 4 y + 35 = 0.
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn
z
−
i
+
1
z
+
i
−
2
là đường thẳng có phương trình A.
2
x
−
3
y
+
1
0
B.
6...
Đọc tiếp
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn z − i + 1 = z + i − 2 là đường thẳng có phương trình
A. 2 x − 3 y + 1 = 0
B. 6 x − 4 y − 3 = 0
C. 2 x − 3 y − 1 = 0
D. 4 x − 6 y + 3 = 0
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn
z
-
i
+
1
z
+
i
-
2
là đường thẳng có phương trình A.
2
x
-
3
y
-
1
0
B.
6
x
-...
Đọc tiếp
Cho i là đơn vị ảo. Tập hợp các điểm biểu diễn hình học số phức thỏa mãn z - i + 1 = z + i - 2 là đường thẳng có phương trình
A. 2 x - 3 y - 1 = 0
B. 6 x - 4 y - 3 = 0
C. 2 x - 3 y + 1 = 0
D. 4 x - 6 y + 3 = 0
Trong không gian tọa độ Oxyz, cho mặt cầu
S
:
x
2
+
y
2
+
z
2
+
4
x
-
6
y
+
m
0
và đường thẳng
∆
là giao tuyến của hai mặt phẳng
α
:
x
+
2
y
-
2...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 + 4 x - 6 y + m = 0 và đường thẳng ∆ là giao tuyến của hai mặt phẳng α : x + 2 y - 2 z - 4 = 0 và β : 2 x - y - z + 1 = 0 . Đường thẳng ∆ cắt mặt cầu (S) tại hai điểm phân biệt A, B thỏa mãn A B = 8 khi:
A. m = 12
B. m = -12
C. m = -10
D. m = 5
Cho số phức z thỏa mãn điều kiện |z|3 Biết rằng tập hợp tất cả các điểm biểu diễn số phức
w
3
-
2
i
+
(
2
-
i
)
z
là một đường tròn. Bán kính của đường tròn đó là A.
R
3
2
B.
R
3
5
C.
R
3
3
D. ...
Đọc tiếp
Cho số phức z thỏa mãn điều kiện |z|=3 Biết rằng tập hợp tất cả các điểm biểu diễn số phức w = 3 - 2 i + ( 2 - i ) z là một đường tròn. Bán kính của đường tròn đó là
A. R = 3 2
B. R = 3 5
C. R = 3 3
D. R = 3 7