Thử cách này  xem.Mình paste luôn ảnh cho bn dễ xem:

Ơ,olm ko cho past cx ko cho gửi link.Đăng link thường vậy:https://imgur.com/If8PtE2

Tham khảo nhé!

ko ai giúp đâu

bài này mk bt lm nhưng mk đag trog trạng thái mệt mỏi nên ngại lắm, để lúc nào rảnh mk giúp bn nhé!

Nếu :  ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;

AM ≤ AC

+ Nếu M  ≡ A hoặc M  ≡  B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.

+ Nếu M nằm giữa B và C; ( M ≢  B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC

+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC

+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH

Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA

Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC

Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤  AB, AM ≤ AC

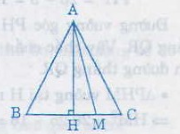
Giả sử   ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;

AM ≤ AC

+ Nếu M  ≡ A hoặc M  ≡  B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.

+ Nếu M nằm giữa B và C; ( M ≢  B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC

+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC

+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH

Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA

Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC

Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤  AB, AM ≤  AC

HÔM NAY, MÌNH VỪA HOÀN THIỆN XONG CÁI TOOL HACK FREE FREE. AI QUAN TÂM THÌ MÌNH SHARE CHO LINK TẢI TOOL NÈ: 
https://bom.to/rHvUS0

Định lý 1: Trong các đường xiên và đường vuông góc kẻ từ một điểm ở ngoài một đường thẳng đến đường thẳng đó, đường vuông góc là đường ngắn nhất.
Định lý 2: Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó;

a) Đường xiên nào có hình chiếu lớn hơn thì lớn hơn

b) Đường xiên nào lớn hơn thì có hình chiếu lớn hơn

c) Nếu hai đường xiên bằng nhau thì hai hình chiếu bằng nhau và ngược lại nếu hai hình chiếu bằng nhau thì hai đường xiên bằng nhau.

Theo hình vẽ các điểm A, B, C, D nằm trên một đường thẳng d và điểm M nằm ngoài đường thẳng đó. MA là đường vuông góc kẻ từ M đến đường thẳng d. Các đoạn thẳng MB, MC, MD là các đường xiên kẻ từ M lần lượt đến B, C và D

Ta có AB, AC, AD lần lượt là hình chiếu của MB, MC, MD xuống d. Ta có ngay AD >AC > AB suy ra

MD > MC >MB > MA

Điều đó có nghĩa là ngày hôm sau bạn Nam bơi đươci xa hơn ngày hôm trước, tức là bạn Nam tập đúng mục đích đề ra

 Ngày hôm sau bạn Nam sẽ bơi được xa hơn ngày hôm trước. Vì MA lần lượt là hình chiếu của MB MC MD mà AB<AC<AD. Vậy Nam sẽ bơi được xa hơn ngày hôm trước

                                 a)              XÉT tam giác HAC (\(\widehat{H}\)=\(90^O\)) CÓ

                                    AH là đường vuông góc của hình xiên AC

                                  \(\Rightarrow AC>AH\) (quan hệ giữa đường vuông góc và hình xiên trong tam giác)      (đpcm)

                            b)                    Xét tam giác HAB (\(\widehat{H}=90^o\)) có

                                          AH là đường vuông góc của đường xiên AB

                                   \(\Rightarrow AB>AH\)(quan hệ giữa đường vuông góc và hình xiên)          (đpcm)

Dựng Δ DBE cân tại D, góc E = DBC = 18° 
=> BD=DE 
ta có ADE = ACB - E = 18° = E nên Δ CED cân tại C 
=> CD = CE. 
Theo hệ thức lượng trong Δ CED: 
DE<CD+CE = 2CD 
mà AC = AD+CD > 2CD (vì AD>CD), và DE = BD 
nên AC>BD 

ta có HB và HC là hai hình chiếu của AB và AC(1)

. Mà tam giác ABC cân tại A => AB=AC(2)

Từ (1) và (2) => HB=HC

ta có AB=AC(tam giác ABC cân)

=> HB=HC ( t/c) (DPCM)