Cho x, y nguyên thoả mãn x2 + 4x + y2 - 12 = 0
Khi đó giá trị lớn nhất P = x2 + y2 là Pmax = ...
Những câu hỏi liên quan
Cho hai số thực x, y thỏa mãn
x
2
-
y
2
+
1
2
+
4
x
2
y
2
-
x
2
-
y
2
0
. Gọi...
Đọc tiếp
Cho hai số thực x, y thỏa mãn x 2 - y 2 + 1 2 + 4 x 2 y 2 - x 2 - y 2 = 0 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức P = x 2 + y 2 . Tính M + m
A. M + m = 3
B. M + m = 5
C. M + m = 2
D. M + m = 4
Cho hai số thực x, y thỏa mãn
x
2
+
y
2
-
4
x
+
6
y
+
4
+
y
2
+
6
y
+
10
6
+
4
x
-
x
2...
Đọc tiếp
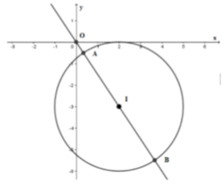
Cho hai số thực x, y thỏa mãn x 2 + y 2 - 4 x + 6 y + 4 + y 2 + 6 y + 10 = 6 + 4 x - x 2 . Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức T = x 2 + y 2 - a . Có bao nhiêu giá trị nguyên thuộc đoạn [-10;10] của tham số a để M ≥ 2 m
A. 17
B. 16
C. 15
D. 18
Chọn B.
Phương pháp:
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
Đúng 0
Bình luận (0)
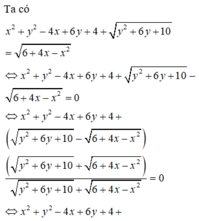
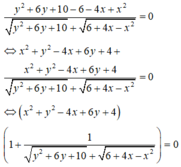
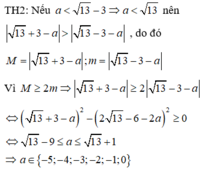
Cho x,y nguyên thỏa mãn 4 x^2+ 4x+ y^2- 12= 0. Khi đó giá trị lớn nhất P= x^2+ y^2 là Pmax=
4x^2 + 4x + y^2 - 12=0
<=> 4x^2 +4x +1 +y^2 -13=0
<=> (2x +1)^2 x + y^2=13 (1)
Vì x; y là số nguyên => (2x +1)^2 ; y^2 là 1 số chính phương
Mà 13=2^2 +3^2
Từ (1) => (2x + 1)^2=2 ^2 ; y^2=3^2 hoặc (2x +1)^2=3^2 ; y^2=2^2
.............
(Tự làm nốt bằng cách tìm ra x; y cụ thể rồi thay vào)
Đúng 0
Bình luận (0)
Xét các số thực x, y thỏa mãn
x
2
+
y
2
1
và
log
x
2
+
y
2
(
2
x
+
3
y
)
≥
1
....
Đọc tiếp
Xét các số thực x, y thỏa mãn x 2 + y 2 > 1 và log x 2 + y 2 ( 2 x + 3 y ) ≥ 1 . Giá trị lớn nhất P m a x của biểu thức P = 2 x + y bằng
Xét các số thực x, y thỏa mãn
x
2
+
y
2
1
và
log
x
2
+
y
2
(
2
x
+
3
y
)
⩾
1
. Giá trị lớn nhất
P
m
a...
Đọc tiếp
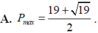
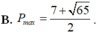
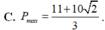
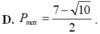
Xét các số thực x, y thỏa mãn x 2 + y 2 > 1 và log x 2 + y 2 ( 2 x + 3 y ) ⩾ 1 . Giá trị lớn nhất P m a x của biểu thức P = 2 x + y bằng:
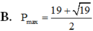
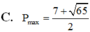
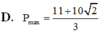
Cho x, y nguyên thỏa mãn x2 + 4x + y2 - 12 = 0. Khi đó giá trị lớn nhất P = x2 + y2 là Pmax =?
x2 +4x+y2-12 =0 => (x+2)2 =(4-y)(4+y) ; vì x;y thuộc Z => 4-y = 4+y => y =0 => (x+2)2 =16
x +2 = 4 => x =2
hoăc x+2 =-4 => x =-6
=> Pmax=x2 +y2 = (-6)2 +0 = 36 khi x = -6; y =0
Đúng 0
Bình luận (0)
Xét các số thực x, y thỏa mãn
x
2
+
y
2
1
và
log
x
2
+
y
2
2
x
+
3
y
≥
1
. Giá trị lớn nhất
P...
Đọc tiếp
Xét các số thực x, y thỏa mãn x 2 + y 2 > 1 và log x 2 + y 2 2 x + 3 y ≥ 1 . Giá trị lớn nhất P m a x của biểu thức P = 2 x + y bằng
A. P m a x = 19 + 19 2
B. P m a x = 7 + 65 2 .
C. P m a x = 11 + 10 2 3
D. P m a x = 7 - 10 2
Xét các số thực x, y thỏa mãn x2 + y2 1 và
log
x
2
+
y
2
2
x
+
3
y
≥
1
. Giá trị l...
Đọc tiếp
Xét các số thực x, y thỏa mãn x2 + y2 > 1 và log x 2 + y 2 2 x + 3 y ≥ 1 . Giá trị lớn nhất Pmax cửa biểu thức P = 2x+y bằng:
A. P m a x = 7 - 10 2
B. P m a x = 19 + 19 2
C. P m a x = 7 + 65 2
D. P m a x = 11 + 10 2 3
Đáp án C.
Phương pháp giải: Dựa vào giả thiết, đánh giá đưa về tổng các bình phương, từ biểu thức P đưa về hạng tử trong tổng bình phương và áp dụng bất đẳng thức Bunhiacopxki tìm giá trị lớn nhất.
Lời giải:
Vì x2 + y2 > 1 suy ra log x 2 + y 2 f ( x ) là hàm số đồng biến trên tập xác định
Khi đó 
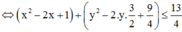
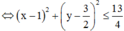
Xét biểu thức P, ta có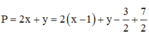 
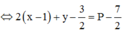
Áp dụng BĐT Bunhiacopxki, có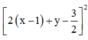 
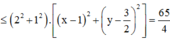
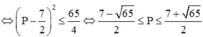
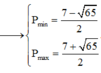
Đúng 0
Bình luận (0)
Cho các số thực x, y thoả mãn x2+y2=5 Tìm Giá Trị Lớn Nhất Của Biểu Thức P= x+2y
\(P-\dfrac{5}{2}=x+2y-\dfrac{x^2+y^2}{2}=-\dfrac{1}{2}\left(x-1\right)^2-\dfrac{1}{2}\left(y-2\right)^2+\dfrac{5}{2}\le\dfrac{5}{2}\)
\(\Rightarrow P-\dfrac{5}{2}\le\dfrac{5}{2}\Rightarrow P\le5\)
\(P_{max}=5\) khi \(\left(x;y\right)=\left(1;2\right)\)
Đúng 1
Bình luận (1)
Cho hàm số y
x
2
− 2(m +
1
m
)x + m (m 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là
y
1
,
y
2
thỏa mãn
y
1
-
y
2
8. Khi đó giá trị của m bằng A. m 1 B. m
∈...
Đọc tiếp
Cho hàm số y = x 2 − 2(m + 1 m )x + m (m > 0) xác định trên [−1; 1]. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên [−1; 1] lần lượt là y 1 , y 2 thỏa mãn y 1 - y 2 = 8. Khi đó giá trị của m bằng
A. m = 1
B. m ∈ ∅
C. m = 2
D. m = 1, m = 2
