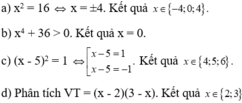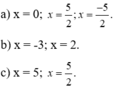`@` `\text {Ans}`

`\downarrow`

`a)`

`-2x (3x + 2)`

`= -6x^2 - 4x`

`b)`

`2/3x(x^2 - x + 4)`

`= 2/3x^3 - 2/3x^2 + 8/3x`

`c)`

`5ab ( ab - 2a^2b^3)`

`= 5a^2b^2 - 10a^3b^4`

`d)`

`3x(x-5)`

`= 3x^2 - 15x`

a) \(A\left(x\right)=x^2-10x+25\)

\(\Rightarrow A\left(x\right)=\left(x-5\right)^2\)

\(\Rightarrow\left\{{}\begin{matrix}A\left(0\right)=\left(0-5\right)^2=25\\A\left(-1\right)=\left(-1-5\right)^2=36\end{matrix}\right.\)

b) \(A\left(x\right)+B\left(x\right)=6x^2-5x+25\)

\(\Rightarrow B\left(x\right)=6x^2-5x+25-A\left(x\right)\)

\(\Rightarrow B\left(x\right)=6x^2-5x+25-\left(x^2-10x+25\right)\)

\(\Rightarrow B\left(x\right)=6x^2-5x+25-x^2+10x-25\)

\(\Rightarrow B\left(x\right)=5x^2+5x\)

\(\Rightarrow B\left(x\right)=5x\left(x+1\right)\)

c) \(A\left(x\right)=\left(x-5\right)C\left(x\right)\)

\(\Rightarrow C\left(x\right)=\dfrac{\left(x-5\right)^2}{x-5}=x-5\left(x\ne5\right)\)

d) Nghiệm của B(x)

\(\Leftrightarrow B=0\)

\(\Leftrightarrow5x\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-1\end{matrix}\right.\) là nghiệm của B(x)

một bể cá dạng hình hộp chữ nhật có chiều dài 1 2 m chiều rộng 0 5 m bên trong có một hòn non bộ  đặc có thể thích bằng 0,09m3 nếu đổ vào 150l nước thì hòn non bộ ngập hoàn toàn trong nước . hỏi chiều cao mực nước ở trong bẻ là bao nhiêu

Lời giải:

Ta thấy:

$(-2a^2b^3)^2\geq 0$ với mọi $a,b$

$(3b^2c^4)^5=3^5(b^5c^{10})^2\geq 0$ với mọi $b,c$ 

Do đó để tổng của chúng bằng $0$ thì:

$-2a^2b^3=b^5c^{10}=0$

$\Rightarrow ab=bc=0$

$\Rightarrow$ (a,b,c)=(a,0,c), (0,b,0)$

a: Ta có: \(x\left(x-3\right)-x^2+5=0\)

\(\Leftrightarrow-3x+5=0\)

hay \(x=\dfrac{5}{3}\)

b: Ta có: \(x^2-6x=0\)

\(\Leftrightarrow x\left(x-6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=6\end{matrix}\right.\)

a: \(\Leftrightarrow\left(x+2\right)\left(x+2-2x+10\right)=0\)

\(\Leftrightarrow x\in\left\{-2;12\right\}\)

a)4x²-9=0

⇔ (2x-3)(2x+3)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{3}{2}\end{matrix}\right.\)

b)(x+5)²-(x-1)²=0

⇔ (x+5-x+1)(x+5+x-1)=0

⇔ 12(x+2)=0

⇔ x=-2

c)x²-6x-7=0

⇔ x²-7x+x-7=0

⇔ x(x-7)+(x-7)=0

⇔ (x-7)(x+1)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x=7\\x=-1\end{matrix}\right.\)

d)(x+1)²-(2x-1)²=0

⇔ (x+1-2x+1)(x+1+2x-1)=0

⇔3x(2-x)=0

\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

a, 4x² - 9 = 0

<=> 4x² = 9

<=> x² = \(\dfrac{9}{4}\) => x = \(\sqrt{\dfrac{9}{4}}\)

b, (x + 5 )² - ( x - 1 )² = 0

<=> ( x+5-x+1 )(x+5+x-1) = 0

<=> 6(2x+4) = 0

<=> 12x+24=0

<=> 12x = -24

<=> x = -2

c, x²-6x-7=0

<=> x²+x-7x-7=0

<=> x(x+1)-7(x+1)=0

<=> (x-7)(x+1)=0

=> x+7=0 hoặc x+1=0

+ x-7=0 => x=7

+ x+1=0 => x=-1

d, \(\left(x+1\right)^2-\left(2x-1\right)^2=0\)

<=> \(\left(x+1-2x+1\right)\left(x+1+2x-1\right)=0\)

<=> (-x+2).3x=0

=> x=0 hoặc (-x+2).3=0

+ (-x+2).3=0 => -3x+6=0 => x=-2

b) (x +5)² -(x -1)²=0

<=> [(x +5) -(x -1)][(x +5) +(x -1)]=0

<=> (x +5 -x +1)(x +5 +x -1)=0

<=> 6(2x+4)=0 <=>12(x +2)=0

=> x +2=0=> x=-2

vậy x= -2

c) x² -6x -7=0

<=> x² -7x +x -7=0

<=> (x² +x)( -7x -7)=0

<=> x(x +1).-7(x +1)=0

<=> (x +1)(x -7)=0

<=> \(\left\{{}\begin{matrix}x+1=0\\x-7=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=-1\\x=7\end{matrix}\right.\)

Vậy S={-1; 7}

d) (x +1)² -(2x -1)²=0

<=> [(x -1)-(2x -1)][(x -1)+(2x -1)]=0

<=> (x -1 -2x +1)(x -1 +2x -1)=0

<=> (x -2x)(3x -2)<=> -x(3x -2)=0

<=> \(\left\{{}\begin{matrix}-x=0\\3x-2=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)

Vậy S={0; \(\dfrac{2}{3}\)}