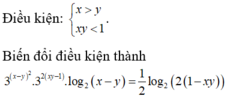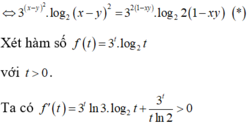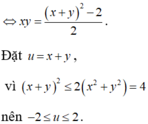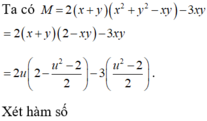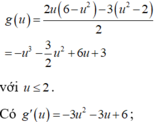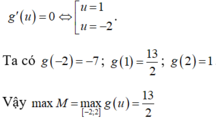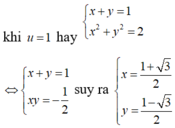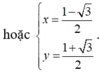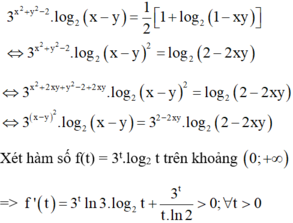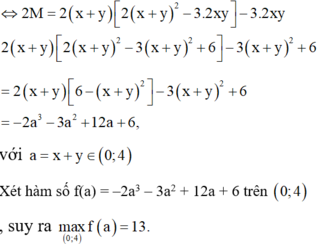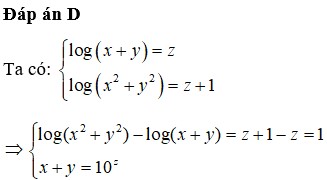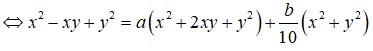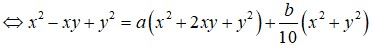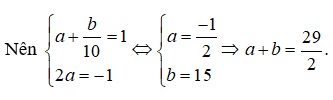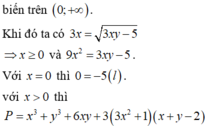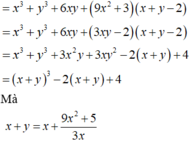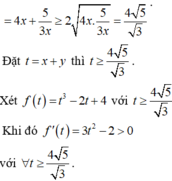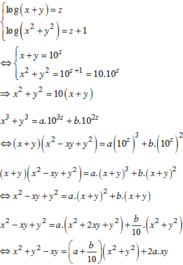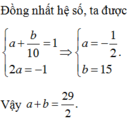cho x, y là các số thực thỏa mãn: x+y=1. tìm GTNN của bt M=x3+y3

Những câu hỏi liên quan
Cho các số thực dương x, y, z thỏa mãn x3 + y3 + z3 = 24. Tìm GTNN của biểu thức
\(M=\dfrac{xyz+2\left(x+y+z\right)^2}{xy+yz+zx}-\dfrac{8}{xy+yz+zx+1}\)
Cho x , y là các số thực thỏa mãn điều kiện:
3
x
2
+
y
2
-
2
.
log
2
x
-
y...
Đọc tiếp
Cho x , y là các số thực thỏa mãn điều kiện: 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 [ 1 + log 2 ( 1 - x y ) ] . Tìm giá trị lớn nhất của biểu thức M = 2 ( x 3 + y 3 ) - 3 x y .
A. 3
B. 7
C. 17 2
D. 13 2
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy (1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P1√1+x2 +1√1+y2 +4xy−x2−y2
Đọc tiếp
Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy =(1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P=1√1+x2 +1√1+y2 +4xy−x2−y2
Không nhìn thấy bất cứ chữ nào của đề bài cả
Đúng 1
Bình luận (0)
Cho x, y là các số thực thỏa mãn điều kiện
3
x
2
+
y
2
-
2
.
log
2
x
-
y
1
2
1
+
log...
Đọc tiếp
Cho x, y là các số thực thỏa mãn điều kiện 3 x 2 + y 2 - 2 . log 2 x - y = 1 2 1 + log 2 1 - x y . Tìm giá trị lớn nhất của biểu thức M = 2(x3 + y3) – xy.
A. 7
B. 13 2
C. 17 2
D. 3
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
10
3
x
+
b
10
2
x
đúng với mọi các số thực dương x, y, z thỏa mãn
log
(
x
+
y...
Đọc tiếp
Giả sử a,b là các số thực sao cho x 3 + y 3 = a 10 3 x + b 10 2 x đúng với mọi các số thực dương x, y, z thỏa mãn log ( x + y ) = z và log ( x 2 + y 2 ) = z + 1 . Giá trị của a+b bằng
A. -31/2
B. -25/2
C. 31/2
D. 29/2
Cho hai số thực x,y thỏa mãn:
9
x
3
+
(
2
-
y
3
x
y
-
5
)
x
+
3
x
y
-...
Đọc tiếp
Cho hai số thực x,y thỏa mãn: 9 x 3 + ( 2 - y 3 x y - 5 ) x + 3 x y - 5 = 0 . Tìm giá trị nhỏ nhất của P = x 3 + y 3 + 6 x y + 3 ( 3 x 2 + 1 ) ( x + y - 2 )
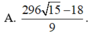
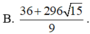
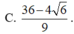
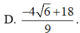
cho x,y là các số thực dương thỏa mãn xy=1 tìm gtnn của bt:
P= \(\left(x+y+1\right)\left(x^2+y^2\right)+\frac{4}{x+y}\)
Giả sử a, b là các số thực sao cho x3 + y3 a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) z và log(x2 + y2) z + 1. Giá trị của a+b bằng: A.
-
31
2
B.
-
25
2
C.
31
2
D.
29
2
Đọc tiếp
Giả sử a, b là các số thực sao cho x3 + y3 = a.103x + b.102x đúng với mọi số thực dương x, y, z thỏa mãn log (x + y) = z và log(x2 + y2) = z + 1. Giá trị của a+b bằng:
A. - 31 2
B. - 25 2
C. 31 2
D. 29 2
Đáp án D.
Ta có
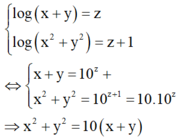
Khi đó
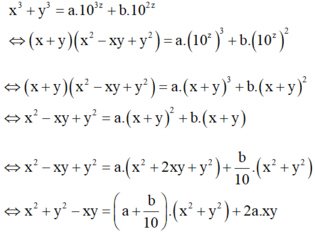
Đồng nhất hệ số, ta được

Đúng 0
Bình luận (0)
Giả sử a,b là các số thực sao cho
x
3
+
y
3
a
.
10
3
x
+
b
.
10
2
x
đúng với mọi số thực dương x,y,z thỏa mãn log(x+y)z và
log
x
2
+...
Đọc tiếp
Giả sử a,b là các số thực sao cho x 3 + y 3 = a . 10 3 x + b . 10 2 x đúng với mọi số thực dương x,y,z thỏa mãn log(x+y)=z và log x 2 + y 2 = z + 1 Giá trị của a+b bằng:
A. -31/2
B. -25/2
C. 31/2
D. 29/2