Câu 7:Biết rằng thì giá trị của
là

Những câu hỏi liên quan
Biết rằng với x = 4 thì hàm số y = 2x + b có giá trị là 5. Vẽ đồ thị của hàm số ứng với giá trị của b tìm được ở câu a.
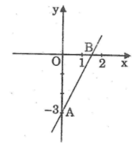
Vẽ đồ thị hàm số y = 2x – 3
Cho x = 0 thì y = -3. Ta có: A(0;-3)
Cho y = 0 thì x = 1,5. Ta có: B(1,5; 0)
Đồ thị của hàm số y = 2x + 3 là đường thẳng đi qua hai điểm A, B
Đúng 0
Bình luận (0)
Câu 1:Số các số tự nhiên thỏa mãn là Câu 2:Biết rằng và . Giá trị của (Nhập kết quả dưới dạng số thập phân đơn giản nhất )Câu 3:Giá trị thỏa mãn là Câu 4:Biết rằng và . Giá trị của (Nhập kết quả dưới dạng số thập phân đơn giản nhất)Câu 5:Cho 2 số thỏa mãn . Giá trị (Nhập kết quả dưới dạng số thập phân đơn giản nhất )Câu 6:Biết rằng và . Giá trị của là (Nhập kết quả dưới dạng số thập phân đơn giản nhất )Câu 7:Giá trị thì biểu thức đạt giá trị lớn nhất.(nhập kết quả dưới dạng số thập...
Đọc tiếp
Câu 1:
Số các số tự nhiên thỏa mãn là
Câu 2:
Biết rằng và . Giá trị của
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 3:
Giá trị thỏa mãn là
Câu 4:
Biết rằng và . Giá trị của
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Câu 5:
Cho 2 số thỏa mãn . Giá trị
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 6:
Biết rằng và . Giá trị của là
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 7:
Giá trị thì biểu thức đạt giá trị lớn nhất.
(nhập kết quả dưới dạng số thập phân gọn nhất)
Câu 8:
Số giá trị thỏa mãn là
Câu 9:
Cho và . Giá trị của
(nhập kết quả dưới dạng số thập phân đơn giản nhất)
Câu 10:
Tập hợp các giá trị nguyên để biểu thức đạt giá trị nhỏ nhất là {}
(Nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ";")
Câu 1:Giá trị của biểu thức tại là Câu 2:Biết đồ thị hàm số đi qua điểm Vậy Câu 3:Giá trị nguyên của thỏa mãn là Câu 4:Tìm biết Trả lời:Câu 5:Tập hợp các số tự nhiên để chia hết cho là {} (Nhập các giá trị theo thứ tự tăng dần,cách nhau bởi dấu ;)Câu 6:Tìm số tự nhiên biết Trả lời:Câu 7:Tập hợp các số nguyên thỏa mãn là {}(Nhập các kết quả theo thứ tự tăng dần,cách nhau bởi dấu ;)Câu 8:Biết rằng thì giá trị của là Câu 9:Số bộ thỏa mãn là Câu 10:Tìm biết: Trả lời:
Đọc tiếp
Câu 1:
Giá trị của biểu thức tại là
Câu 2:
Biết đồ thị hàm số đi qua điểm Vậy
Câu 3:
Giá trị nguyên của thỏa mãn là
Câu 4:
Tìm biết
Trả lời:
Câu 5:
Tập hợp các số tự nhiên để chia hết cho là {}
(Nhập các giá trị theo thứ tự tăng dần,cách nhau bởi dấu ";")
Câu 6:
Tìm số tự nhiên biết
Trả lời:
Câu 7:
Tập hợp các số nguyên thỏa mãn là {}(Nhập các kết quả theo thứ tự tăng dần,cách nhau bởi dấu ";")
Câu 8:
Biết rằng thì giá trị của là
Câu 9:
Số bộ thỏa mãn là
Câu 10:
Tìm biết:
Trả lời:
Câu 1:Số các số tự nhiên thỏa mãn là Câu 2:Biết rằng và . Giá trị của (Nhập kết quả dưới dạng số thập phân đơn giản nhất )Câu 3:Biết rằng và . Giá trị của (Nhập kết quả dưới dạng số thập phân đơn giản nhất)Câu 4:Tập hợp các giá trị thỏa mãn: là {}(Nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ;)Câu 5:Số giá trị thỏa mãn là Câu 6:Biết rằng và . Giá trị của là (Nhập kết quả dưới dạng số thập phân đơn giản nhất )Câu 7:Cho 2 số thỏa mãn . Giá trị (Nhập kết quả dưới dạng s...
Đọc tiếp
Câu 1:
Số các số tự nhiên thỏa mãn là
Câu 2:
Biết rằng và . Giá trị của
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 3:
Biết rằng và . Giá trị của
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Câu 4:
Tập hợp các giá trị thỏa mãn: là {}
(Nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ";")
Câu 5:
Số giá trị thỏa mãn là
Câu 6:
Biết rằng và . Giá trị của là
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 7:
Cho 2 số thỏa mãn . Giá trị
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 8:
Giá trị nhỏ nhất của biểu thức là
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Câu 9:
Tập hợp các giá trị nguyên để biểu thức đạt giá trị nhỏ nhất là {}
(Nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ";")
Câu 10:
Cho và . Giá trị của
(nhập kết quả dưới dạng số thập phân đơn giản nhất)
cho biết x và y là 2 đại lượng tỉ lệ nghịch bt rằng khi x=7 thì y =4 khi đó nếu x=2 giá trị của y là
k=28
=>y=28/x
Khi x=2 thì y=14
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tim phân số có tử là -7, biết rằng khi nhân tử với 3 và cộng mẫu với 26 thì giá trị của phân số không thay đổi.
Phân số phải tìm có dạng − 7 x ( x ∈ Z ; x ≠ 0 )
Theo đề bài ta có:
− 7 x = − 7.3 x + 26 ⇒ − 7.3 x .3 = − 7.3 x + 26 ⇒ 3. x = x + 26 x = 13
Đúng 0
Bình luận (0)
Biết rằng
Q
x
2
-
6
x
+
9
x
2
-
9
x
-
3
2
x...
Đọc tiếp
Biết rằng Q = x 2 - 6 x + 9 x 2 - 9 = x - 3 2 x - 3 x + 3 = x - 3 x + 3
Hãy tính giá trị của biểu thức Q. Câu trả lời nào sau đây là sai ?
A. Giá trị của Q tại x = 4 là (4 - 3)/(4 + 3) = 1/7
B. Giá trị của Q tại x = 1 là (1 - 3)/(1 + 3) = (-1)/2
C. Giá trị của Q tại x = 3 là (3 - 3)/(3 + 3) = 0
D. Giá trị của Q tại x = 3 không xác định.
Chọn đáp án C
Giá trị của biểu thức Q = x 2 - 6 x + 9 x 2 - 9 = x - 3 2 x - 3 x + 3 = x - 3 x + 3
Giá trị của Q tại x = 3 là (3-3)/(3+3) = 0 sai vì x = 3 phân thức đã cho không xác định.
Đúng 0
Bình luận (0)
Tìm một số biết rằng nếu cộng cả tử và mẫu của phân số 7/23 với số đó thì được phân số mới có giá trị bằng 7/9? Số cần tìm là:
Nếu cộng cả tử và mẫu với một số thì hiệu tử và mẫu vẫn không đổi
Hiệu tử và mẫu là :
`23-7=16`
Coi tử số có giá trị 7 phần, mẫu số 9 phần
Hiệu số phần :
`9-7=2` (phần)
Tử số sau khi cộng thêm :
\(16:2\times7=56\)
SPT là :
`56-7=49`
Đúng 1
Bình luận (0)
khi ta cộng tử số và mẫu số với cùng một số thì hiệu của mẫu số và tử số lúc sau không đổi và bằng:
23 - 7 = 16
Theo bài ra ta có sơ đồ:

Theo sơ đồ ta có:
Tử số lúc sau là:
16: (9-7) \(\times\) 7 = 56
Vậy số cần thêm vào tử số và mẫu số là:
56 - 7 = 49
Đáp số: 49
Đúng 3
Bình luận (0)
Câu 1:Tập hợp các giá trị thỏa mãn: là {}(Nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ;)Câu 2:Hai đường thẳng song song, một cát tuyến cắt hai đường thẳng tạo ra cặp góc trong cùng phía hơn kém nhau . Số đo hai góc lần lượt là (tính theo độ, nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ;)Câu 3:Giá trị thỏa mãn là Câu 4:Biết rằng và . Giá trị của (Nhập kết quả dưới dạng số thập phân đơn giản nhất )Câu 5:Giá trị thì biểu thức đạt giá trị lớn nhất.(nhập kết quả...
Đọc tiếp
Câu 1:
Tập hợp các giá trị thỏa mãn: là {}
(Nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ";")
Câu 2:
Hai đường thẳng song song, một cát tuyến cắt hai đường thẳng tạo ra cặp góc trong cùng phía hơn kém nhau . Số đo hai góc lần lượt là (tính theo độ, nhập kết quả theo giá trị tăng dần, ngăn cách nhau bởi dấu ";")
Câu 3:
Giá trị thỏa mãn là
Câu 4:
Biết rằng và . Giá trị của
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 5:
Giá trị thì biểu thức đạt giá trị lớn nhất.
(nhập kết quả dưới dạng số thập phân gọn nhất)
Câu 6:
Giá trị nhỏ nhất của biểu thức là
(Nhập kết quả dưới dạng số thập phân đơn giản nhất)
Câu 7:
Biết rằng và . Giá trị của là
(Nhập kết quả dưới dạng số thập phân đơn giản nhất )
Câu 8:
Số giá trị thỏa mãn là
Câu 9:
Số tự nhiên thỏa mãn là
Hãy điền dấu >; < ; = vào chỗ ... cho thích hợp nhé !
Câu 10:
So sánh:
Cho a và b là hai đại lượng tỉ lệ thuận với nhau.biết rằng khi a = 3 thì b= 33
a.Tìm hệ số tỉ lệ của a đối với b
b.Tính giá trị của a khi b = -7
c.Tính giá trị của b khi a =110
Bạn nào biết thì giúp mình với mình đang cần gấp!
`a,`
Vì `a` và `b` là `2` đại lượng tỉ lệ thuận
`\rightarrow a=k*b`
Thay `a=3, b=33`
`\rightarrow 3=k*33`
`\rightarrow k=3 \div 33`
`\rughtarrow k=`\(\dfrac{1}{11}\)
Vậy, hệ số tỉ lệ `k=`\(\dfrac{1}{11}\)
`b,`
Khi `b=-7 \rightarrow a=`\(\dfrac{1}{11}\cdot-7=-\dfrac{7}{11}\)
`,`
Khi `a=110 \rightarrow b= 110 \div`\(\dfrac{1}{11}\)`= 1210`
Đúng 1
Bình luận (0)
Lời giải:
a. Gọi $k$ là hệ số tỉ lệ của $a$ đối với $b$. Ta có: $a=bk$
$\Rightarrow k=\frac{a}{b}=\frac{3}{33}=\frac{1}{11}$
b. Ta có: $a=\frac{b}{11}$
Khi $b=-7$ thì $a=\frac{b}{11}=\frac{-7}{11}$
c. $110=a=\frac{b}{11}\Rightarrow b=110.11=1210$
Đúng 1
Bình luận (0)























