Cho tam giác ABC có I(-1;2) là trung điểm của cạnh BC . M(3;-2) là trung điểm của cạnh AC Gọi A'(4;-5) là điểm đối xứng với A qua điểm I.Tìm tọa độ các điểm của tam giác ABC.
Lưu ý:Chỉ sử dụng đến trọng tâm trung điểm
Trong mp xOy cho tam giác ABC. bt A(3;-1) B(-1;2) I(1;-1) là trọng tâm của tam giác ABC. Trực tâm H của tam giác ABC có tọa độ (a;b). Tính a+3b
Tọa độ điểm C:
\(\left\{{}\begin{matrix}x_C=3x_I-x_A-x_B=1\\y_C=3y_I-y_A-y_B=-4\end{matrix}\right.\Rightarrow C\left(1;-4\right)\)
Ta có:
\(\overrightarrow{AH}=\left(a-3;b+1\right)\)
\(\overrightarrow{BH}=\left(a+1;b-2\right)\)
\(\overrightarrow{BC}=\left(2;-6\right)\)
\(\overrightarrow{AC}=\left(-2;-3\right)\)
Theo giả thiết
\(AH\perp BC\Rightarrow2\left(a-3\right)-6\left(b+1\right)=0\Leftrightarrow a-3b=6\left(1\right)\)
\(BH\perp AC\Rightarrow-2\left(a+1\right)-3\left(b-2\right)=0\Leftrightarrow2a+3b=4\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow\left\{{}\begin{matrix}a=\dfrac{10}{3}\\b=-\dfrac{8}{9}\end{matrix}\right.\Rightarrow a+3b=\dfrac{2}{3}\)
Cho tam giác ABC có A(-1; 1), B(3; 1), C(2; 4) . Tìm tọa độ điểm I là tâm đường tròn ngoại tiếp tam giác ABC.
A. I( 1; 2)
B. I(2; 1)
C. I(1; 1)
D. I(2; 2)
Chọn A.
Gọi I(x; y) là tâm đường tròn ngoại tiếp ΔABC
Suy ra 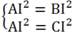
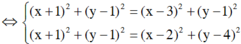
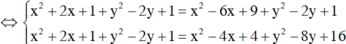
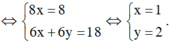
Cho tam giác ABC trên AB lấy điểm D sao cho BD bằng 1/3 AD. Nối D với C. Trên DC lấy điểm I sao cho IC bằng 1/3 DC. Tính diện tích tam giác ADI. Biết diện tích tam giác ABC là 120 cm2
Cho tam giác ABC trên BC lấy điểm D sao cho BC bằng DC. Nối A với D.Trên AD lấy điểm I sao cho I là trung điểm cạnh AD. Nối B với I, C với I. Chỉ ra các cặp tam giác có dện tích bằng nhau
Cho tam giấc BC. Trên cạnh BC lấy D sao cho BD 25 x BC. Trên AD lấy AM 23 x AD. Tính diện tích tam giác ABM biết diện tích ABC là 54 cm2
Cho tam giác ABC có chu vi là 10 cm, giao điểm I của các đường phân giác các cạnh 1 cm. Tính diện tích tam giác ABC
Bài 1:Cho tam giác ABC cân tại A,đường cao AM,gọi I là trung điểm AC,K là điểm đối xứng M qua I a)Chứng minh rằng:Tứ giác AMCK là hình chữ nhật b)Cho AB=13cm,BC=10cm.Tính diện tích tam giác ABC Bài 2:Cho tam giác ABC vuông tại A có AB<AC.Gọi M là trung điểm BC.Từ M kẻ MD vuông góc với AC tại D,kẻ ME vuông góc với AB tại E a)Chứng minh tứ giác ADME là HCN b)Gọi P là điểm đối xứng của D qua M,Q là điểm đối xứng của E qua M.Chứng minh DEPQ là hình thoi Bài 3: Cho tam giác ABC nhọn(AB>AC)có AK là đường cao,gọi N là trung điểm AB,lấy F đối xứng K qua N. a)Chứng minh:Tứ giác AKBF là HCN b)Gọi E đối xứng N qua FB,T là giao điểm NE và FB.Chứng minh NFEB là hình thoi
Bài 1:
a: Xét tứ giác AMCK có
I là trung điểm của AC
I là trung điểm của MK
Do đó: AMCK là hình bình hành
mà \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
b: BH=BC/2=5(cm)
=>AH=12cm
\(S_{ABC}=\dfrac{AH\cdot BC}{2}=\dfrac{12\cdot10}{2}=60\left(cm^2\right)\)
Cho tam giác abc có bd và ce là phân giác cắt nhau tại i . cmr: nếu bi*ci=1/2 bd*ce thì tam giác abc vuông
Cho Tam giác ABC có D nằm trên AB sao cho AB=1/2DB.Trên ÁC lấy E sao cho AE =2EC . BE cắt CD tại i a)So sánh diện tích Tam giác ABC và diện tích Tam giác BEC b)Tính diện tích Tam giác BIC biết diện tích Tam giác ADI =10cm2
Sửa đề: \(AD=\frac12\times DB\)
a: Ta có: AE+EC=AC
=>AC=2EC+EC=3EC
=>\(S_{ABC}=3\times S_{BEC}\)
b: Ta có; AE=2xEC
=>\(S_{BEA}=2\times S_{BEC};S_{IEA}=2\times S_{IEC}\)
=>\(S_{BEA}-S_{IEA}=2\times\left(S_{BEC}-S_{IEC}\right)\)
=>\(S_{BIA}=2\times S_{BIC}\)
Ta có: \(AD=\frac12\times DB\)
=>\(S_{CDA}=\frac12\times S_{CDB};S_{IDA}=\frac12\times S_{IDB}\)
=>\(S_{CDA}-S_{IDA}=\frac12\times\left(S_{CDB}-S_{IDB}\right)\)
=>\(S_{CIA}=\frac12\times S_{CIB}\)
Ta có: \(S_{AIB}+S_{AIC}+S_{BIC}=S_{ABC}\)
=>\(S_{BIC}+2\times S_{BIC}+\frac12\times S_{BIC}=S_{ABC}\)
=>\(S_{ABC}=3,5\times S_{BIC}\)
Ta có: \(AD=\frac12\times DB\)
=>\(S_{ADI}=\frac12\times S_{IDB}\)
=>\(S_{IDB}=10\times2=20\left(\operatorname{cm}^2\right)\)
\(S_{AIB}=S_{IDA}+S_{IDB}=10+20=30\left(\operatorname{cm}^2\right)\)
=>\(S_{BIC}=\frac{30}{2}=15\left(\operatorname{cm}^2\right)\)
cho tam giác ABC có lấy B và C làm tâm vẽ hai cung tròn có bán kính bằng nhau, sao cho hai cùng này cắt nhau tại 1 điểm i nằm trong tam giác ABC
cm: ba điểm A, I, N thẳng hàngCho tam giác ABC vuông đỉnh A có AB=AC. Điểm I nằm trong tam giác ABC sao cho IA : IB : IC = 2:3:1. Tính số đo góc AIC.
cho tam giác ABC có A(-1;1) ; B(1;3) ; C(1;-1)
a , tam gisc ABC là tam giác gì , tính chu vi và diện tích .
b , tìm tọa độ tâm I và tính bán kính đường tròn ngoại tiếp tam giác ABC
c , tìm tọa độ điểm D có hoành độ âm sao cho tam giác ADC vuông cân tại D .