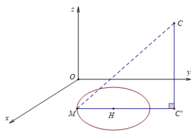
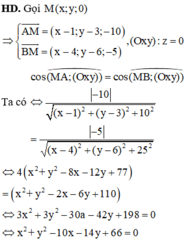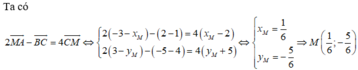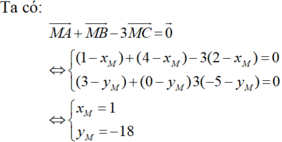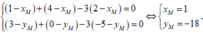Trong các mặt phẳng tạo độ Oxy cho các điểm A(5;4), B(2;3),C(6;1) số đo của góc BAC bằng bao nhiêu

Những câu hỏi liên quan
Trong không gian tọa độ Oxyz, cho A(1;3;10), B(4;6;5) và M là điểm thay đổi trên mặt phẳng (Oxy) sao cho MA, MB cùng tạo với mặt phẳng (Oxy) các góc bằng nhau. Tìm giá trị nhỏ nhất của AM
A. 6 3 6
B. 10
C. 10
D. 8 2
Trong mặt phẳng tọa độ Oxy, cho các điểm A(5; 4), B(2; 3), C(6; 1). Số đo BAC = .... độ
90 độ nha bn cái này mk làm oy!!
Đúng 0
Bình luận (0)
bn vẽ hình ra là sẽ thấy BAC là góc vuông =>BAC=900,mk lười vẽ quá
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho các điểm A(-3; 3) ; B(1; 4) ; C( 2; -5). Tọa độ điểm M thỏa mãn
2
M
A
→
-
B
C
→
4
C
M
→
là: A. B. C. D.
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm A(-3; 3) ; B(1; 4) ; C( 2; -5). Tọa độ điểm M thỏa mãn 2 M A → - B C → = 4 C M → là:
A. 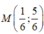
B. ![]()
C. 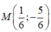
D. 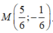
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A. M(1; -18). B. M(1 ;18). C. M(18; -1). D. M(-18; -1).
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A. M(1; -18).
B. M(1 ;18).
C. M(18; -1).
D. M(-18; -1).
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ;; B( 4; 0) ; C( 2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A.M( 1; -18) B.M( 1 ;18) C.M( 18; -1 D.M(...
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ;; B( 4; 0) ; C( 2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A.M( 1; -18)
B.M( 1 ;18)
C.M( 18; -1
D.M( -18; -1)
Trong không gian Oxyz, cho các điểm A(4;-2;4), B(-2;6;4), C(5;-1;-6). Xét các điểm M thuộc mặt phẳng (Oxy) sao cho
A
M
B
^
90
°
, đoạn thẳng CD có độ dài lớn nhất bằng A.
73
B.
5
3
C. 10 D. 8
Đọc tiếp
Trong không gian Oxyz, cho các điểm A(4;-2;4), B(-2;6;4), C(5;-1;-6). Xét các điểm M thuộc mặt phẳng (Oxy) sao cho A M B ^ = 90 ° , đoạn thẳng CD có độ dài lớn nhất bằng
A. 73
B. 5 3
C. 10
D. 8
. Trong mặt phẳng Oxy . cho tam giác ABC, biết A(2;3) , B(-5;-1), C(3;-2)
1) Tìm tọa độ trung điểm I của đoạn cạnh AB và tọa độ trọng tâm G của tâm giác ABC
2) Tính độ dài các đoạn thẳng CI và AG
3) Tìm tạo độ điểm D sao cho tứ giác ABCD là hình bình hành
4) Tìm tọa độ trục tâm H của tam giác ABC
1.
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-\dfrac{3}{2}\\y_I=\dfrac{y_A+y_B}{2}=1\end{matrix}\right.\) \(\Rightarrow I\left(-\dfrac{3}{2};1\right)\)
\(\left\{{}\begin{matrix}x_G=\dfrac{x_A+x_B+x_C}{3}=0\\y_G=\dfrac{y_A+y_B+y_C}{3}=0\end{matrix}\right.\) \(\Rightarrow G\left(0;0\right)\)
2.
\(\left\{{}\begin{matrix}\overrightarrow{CI}=\left(-\dfrac{9}{2};3\right)\\\overrightarrow{AG}=\left(-2;-3\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}CI=\sqrt{\left(-\dfrac{9}{2}\right)^2+3^2}=\dfrac{3\sqrt{13}}{2}\\AG=\sqrt{\left(-2\right)^2+\left(-3\right)^2}=\sqrt{13}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
3.
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-7;-4\right)\\\overrightarrow{DC}=\left(3-x;-2-y\right)\end{matrix}\right.\)
\(ABCD\) là hbh \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow\left\{{}\begin{matrix}-7=3-x\\-4=-2-y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=10\\y=2\end{matrix}\right.\)
\(\Rightarrow D\left(10;2\right)\)
4. Gọi \(H\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{CH}=\left(x-3;y+2\right)\\\overrightarrow{AH}=\left(x-2;y-3\right)\\\overrightarrow{BC}=\left(8;-1\right)\end{matrix}\right.\)
H là trực tâm \(\Leftrightarrow\left\{{}\begin{matrix}AH\perp BC\\CH\perp AB\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AH}.\overrightarrow{BC}=0\\\overrightarrow{CH}.\overrightarrow{AB}=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8\left(x-2\right)-1\left(y-3\right)=0\\-7\left(x-3\right)-4\left(y+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x-y=13\\-7x-4y=-13\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{3};\dfrac{1}{3}\right)\)
Đúng 2
Bình luận (0)
Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A ( 1 ; 2) , B ( 3 ; 4 ) , C ( 6 ; -5 )
a)Tính toán các cạnh và số đo các góc của tam giác ABC
\(AB=\sqrt{\left(3-1\right)^2+\left(4-2\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(6-1\right)^2+\left(-5-2\right)^2}=\sqrt{74}\)
\(BC=\sqrt{\left(6-3\right)^2+\left(-5-4\right)^2}=3\sqrt{10}\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{-\sqrt{37}}{37}\)
=>góc A=99 độ
AB/sinC=AC/sinB=BC/sinA
=>\(\dfrac{3\sqrt{10}}{sin99}=\dfrac{2\sqrt{2}}{sinC}=\dfrac{\sqrt{74}}{sinB}\)
=>góc C=17 độ; góc B=64 độ
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: A = T v → ( M )
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: M = T v → ( A )
Giả sử A = (x; y). Khi đó

Vậy A = (1; 3)
Đúng 0
Bình luận (0)