Từ đồ thị ta thấy \(f'\left(x\right)>0\) trên các khoảng \(\left(-1;1\right)\) và \(\left(3;+\infty\right)\)

\(f'\left(x\right)< 0\) trên \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)

\(\Rightarrow\) Hàm nghịch biến trên (1;3)

Chọn B

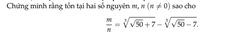
Đặt \(x=\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\)

\(x^3=14-3\sqrt[3]{\left(\sqrt[]{50}+7\right)\left(\sqrt[]{50}-7\right)}\left(\sqrt[3]{\sqrt[]{50}+7}-\sqrt[3]{\sqrt[]{50}-7}\right)\)

\(x^3=14-3x\)

\(x^3+3x-14=0\)

\(\left(x-2\right)\left(x^2+2x+7\right)=0\)

\(x=2\)

\(\Rightarrow\dfrac{m}{n}=2\)

\(\Rightarrow\) Hiển nhiên tồn tại vô số m, n nguyên thỏa mãn đẳng thức trên

a: Δ=(m-2)^2-4(m-4)

=m^2-4m+4-4m+16

=m^2-8m+20

=m^2-8m+16+4

=(m-2)^2+4>=4>0

=>Phương trình luôn có 2 nghiệm pb

b: x1^2+x2^2

=(x1+x2)^2-2x1x2

=(m-2)^2-2(m-4)

=m^2-4m+4-2m+8

=m^2-6m+12

=(m-3)^2+3>=3

Dấu = xảy ra khi m=3

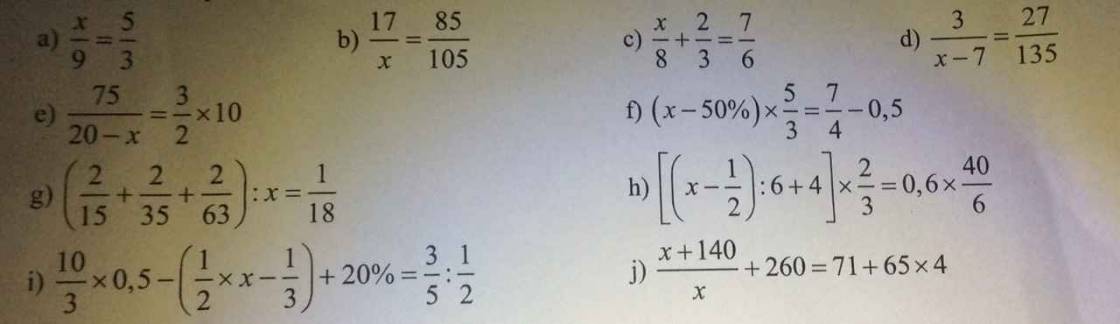
\(a,\dfrac{x}{9}=\dfrac{5}{3}\\ \Leftrightarrow x=9\cdot\dfrac{5}{3}\\ \Leftrightarrow x=15\\ b,\dfrac{17}{x}=\dfrac{85}{105}\\ \Leftrightarrow x=17\cdot\dfrac{105}{85}\\ \Leftrightarrow x=21\\ c,\dfrac{x}{8}+\dfrac{2}{3}=\dfrac{7}{6}\\ \Leftrightarrow\dfrac{x}{8}=\dfrac{1}{2}\\ \Leftrightarrow x=4\\ d,\dfrac{3}{x-7}=\dfrac{27}{135}\\ \Leftrightarrow x-7=15\\ \Leftrightarrow x=22\)

\(e,\dfrac{75}{20-x}=\dfrac{3}{2}\times10\\ \Leftrightarrow\dfrac{75}{20-x}=15\\ \Leftrightarrow20-x=5\\ \Leftrightarrow x=15\\ f,\left(x-50\%\right)\times\dfrac{5}{3}=\dfrac{7}{4}-0,5\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)\times\dfrac{5}{3}=\dfrac{5}{4}\\ \Leftrightarrow x-\dfrac{1}{2}=\dfrac{3}{4}\\ \Leftrightarrow x=\dfrac{5}{4}\\ g,\left(\dfrac{2}{15}+\dfrac{3}{35}+\dfrac{2}{63}\right):x=\dfrac{1}{18}\\ \Leftrightarrow\dfrac{2}{9}:x=\dfrac{1}{18}\\ \Leftrightarrow x=4\)

\(h,\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=0,6\times\dfrac{40}{6}\\ \Leftrightarrow\left[\left(x-\dfrac{1}{2}\right):6+4\right]\times\dfrac{2}{3}=4\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6+4=6\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right):6=2\\ \Leftrightarrow x-\dfrac{1}{2}=12\\ \Leftrightarrow x=\dfrac{25}{2}\)

\(i,\dfrac{10}{3}\times0,5-\left(\dfrac{1}{2}\times x-\dfrac{1}{3}\right)+20\%=\dfrac{3}{5}:\dfrac{1}{2}\\ \Leftrightarrow\dfrac{5}{3}-\dfrac{1}{2}x+\dfrac{1}{3}+\dfrac{1}{5}=\dfrac{6}{5}\\ \Leftrightarrow\dfrac{1}{2}x=1\\ \Leftrightarrow x=2\)

\(j,\dfrac{x+140}{x}+260=71+65\times4\\ \Leftrightarrow\dfrac{x+140}{x}=71\\ \Leftrightarrow x+140=71x\\ \Leftrightarrow70x=140\\ \Leftrightarrow x=2\)

\(y=\dfrac{sinx-cosx}{sinx+cosx}\Rightarrow y'=\dfrac{\left(sinx-cosx\right)'.\left(sinx+cosx\right)-\left(sinx+cosx\right)'.\left(sinx-cosx\right)}{\left(sinx+cosx\right)^2}\)

Dễ thấy : \(\left(sinx-cosx\right)'=cosx+sinx\)

\(\left(sinx+cosx\right)'=cosx-sinx\)

Suy ra : \(y'=\dfrac{\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2}{\left(sinx+cosx\right)^2}=\dfrac{2}{\left(sinx+cosx\right)^2}\)

3.15:
EF vuông góc MH

NP vuông góc MH

Do đó: EF//NP

3.17:

góc yKH+góc H=180 độ

mà hai góc này là hai góc ở vị trí trong cùng phía

nên Ky//Hx

3.

Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)

B đúng

4.

Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)

A đúng

1.

B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)

Câu 2 đề thiếu yêu cầu

Câu 9:

Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)

\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)