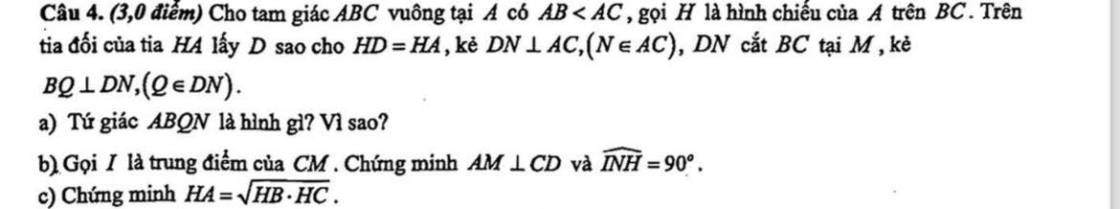Mn vẽ đáy ABC NẰM DƯỚI NHÉ Ạ. MN CHỈ CẦN XÁC ĐỊNH GÓC THÔI

Những câu hỏi liên quan
giúp em các bài 10,13,20 với mn ơi em chỉ cần trình bày thôi ạ nếu có hình vẽ thì càng tốt ạ
Mọi người giải giúp mình bài này với ạ, cảm ơn mn nhiều, chỉ cần câu c ý chứng minh góc 90 độ thôi ạ
a: Xét tứ giác ABQN có
\(\widehat{BQN}=\widehat{QNA}=\widehat{NAB}=90^0\)
=>ABQN là hình chữ nhật
b: Xét ΔCAD có
DN,CH là các đường cao
DN cắt CH tại M
Do đó: M là trực tâm của ΔCAD
=>AM\(\perp\)CD
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
\(\widehat{HAB}=\widehat{HCA}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔHAB đồng dạng với ΔHCA
=>\(\dfrac{HA}{HC}=\dfrac{HB}{HA}\)
=>\(HA^2=HB\cdot HC\)
=>\(HA=\sqrt{HB\cdot HC}\)
Đúng 1
Bình luận (3)
Cho (O ;R) từ điểm A nằm ngoài (O)vẽ hai tiếp tuyến AB AC và các tiếp tuyến AMN a) Chứng minh AM.AN AB^2 b) Vẽ đường kính BD chứng minh CD//OA C) cho MN 8 cm ; R 5cm . Tính khoảng cách từ O đến dây MN D) BC cắt OA tại H, c/m AH.ADAM.AN E) c/m tứ giác ABOC nội tiếp đường tròn .Xác định tâm I và bán kính của đường tròn đó Câu a , b, c , d mình làm rồi mình chỉ cần câu e thôi ai biết chỉ mình vs thanks
Đọc tiếp
Cho (O ;R) từ điểm A nằm ngoài (O)vẽ hai tiếp tuyến AB AC và các tiếp tuyến AMN a) Chứng minh AM.AN = AB^2 b) Vẽ đường kính BD chứng minh CD//OA C) cho MN = 8 cm ; R = 5cm . Tính khoảng cách từ O đến dây MN D) BC cắt OA tại H, c/m AH.AD=AM.AN E) c/m tứ giác ABOC nội tiếp đường tròn .Xác định tâm I và bán kính của đường tròn đó Câu a , b, c , d mình làm rồi mình chỉ cần câu e thôi ai biết chỉ mình vs thanks
Vì \(\widehat{ABO}\)là góc tạo bởi tia tiếp tuyến AB và dây cung BD ( đường kính AB )
\(\Rightarrow\widehat{ABO}=\frac{1}{2}.\widehat{BOD}=\frac{1}{2}.180^o=90^o\)
Chứng mình ương tự với \(\widehat{ACO}\), suy ra \(\widehat{ACO}=90^o\)
Xét tứ giác ABOC có :
Góc ABO và góc ACO là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=90^o+90^o=180^o\)
=> Tứ giác ABOC nội tiếp đường tròn ( theo tính chất tổng hai góc đối bằng 180 độ ... )
Gọi I là trung điểm của AB
Có tam giác ABO vuông tại B, trung tuyến là BI
=> BI = 1/2.AO=AI=IO (1)
Tam giác ACO vuông tại C, có trung tuyến là CI
=> CI=1/2.AO=AI=IO (2)
Từ (1) và (2) => BI = AI = IO = IC
=> I cách đều 4 đỉnh tứ giác ABOC
=> I là tâm đường tròn ngoại tiếp tứ giác ABOC , có bán kinh R= 1/2.AO
MN GIÚP MIK CÂU Ý 3 THÔI Ạ
MIK CHỈ CẦN Ý 3 THÔI Ạ
KO CẦN Ý 1,2 Ạ
Bài 1: cho \(\Delta ABC\) vuông tại A C có AB=AC. Qua A kẻ đường thẳng xy ( B,C nằm cùng phía với xy ). Kẻ BD và CE vuông góc với xy. Chứng minh rằng :
a) \(\Delta BAD=\Delta ACE\)
b) DE=BD+CE
mn chỉ cần giải thôi nhé ![]() ko cần vẽ hình
ko cần vẽ hình
Mình chỉ cần câu c thôi ạ, không hình cũng được ạ. Mình cảm ơn
Cho A nằm ngoài (O;R) vẽ hai tiếp tuyến AB,AC.
a. chứng minh OA vuông góc BC.
b. vẽ đường kinh CD, AD cắt (O) tại N. chứng minh AH.AO= AN.AD
c. giả sử OA=2R. tính giá trị chính xác sin(AHN)
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC
b: Xét (O) có
ΔCND nội tiếp
CD là đường kính
Do đó: ΔCND vuông tại N
=>CN\(\perp\)ND tại N
=>CN\(\perp\)AD tại N
Xét ΔDCA vuông tại C có CN là đường cao
nên \(AN\cdot AD=AC^2\left(3\right)\)
Ta có: OA là trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOCA vuông tại C có CH là đường cao
nên \(AH\cdot AO=AC^2\left(4\right)\)
Từ (3) và (4) suy ra \(AN\cdot AD=AH\cdot AO\)
c: Ta có: \(AH\cdot AO=AN\cdot AD\)
=>\(\dfrac{AH}{AD}=\dfrac{AN}{AO}\)
Xét ΔAHN và ΔADO có
\(\dfrac{AH}{AD}=\dfrac{AN}{AO}\)
\(\widehat{HAN}\) chung
Do đó: ΔAHN đồng dạng với ΔADO
=>\(\widehat{AHN}=\widehat{ADO}\)
Ta có: ΔOCA vuông tại C
=>\(CO^2+CA^2=OA^2\)
=>\(CA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Ta có: ΔDCA vuông tại C
=>\(DC^2+CA^2=DA^2\)
=>\(DA^2=\left(2R\right)^2+\left(R\sqrt{3}\right)^2=7R^2\)
=>\(DA=R\sqrt{7}\)
Xét ΔDCA vuông tại C có \(sinCDA=\dfrac{CA}{DA}\)
=>\(sinCDA=\dfrac{R\sqrt{3}}{R\sqrt{7}}=\sqrt{\dfrac{3}{7}}=\dfrac{\sqrt{21}}{7}\)
=>\(sinAHN=\dfrac{\sqrt{21}}{7}\)
Đúng 1
Bình luận (0)
Mn giair dùm minh câu này với ạ
Tìm tất cả độ dài tất cả các cạnh và góc
Chỉ cần tìm câu b) thôi. Thxxxx

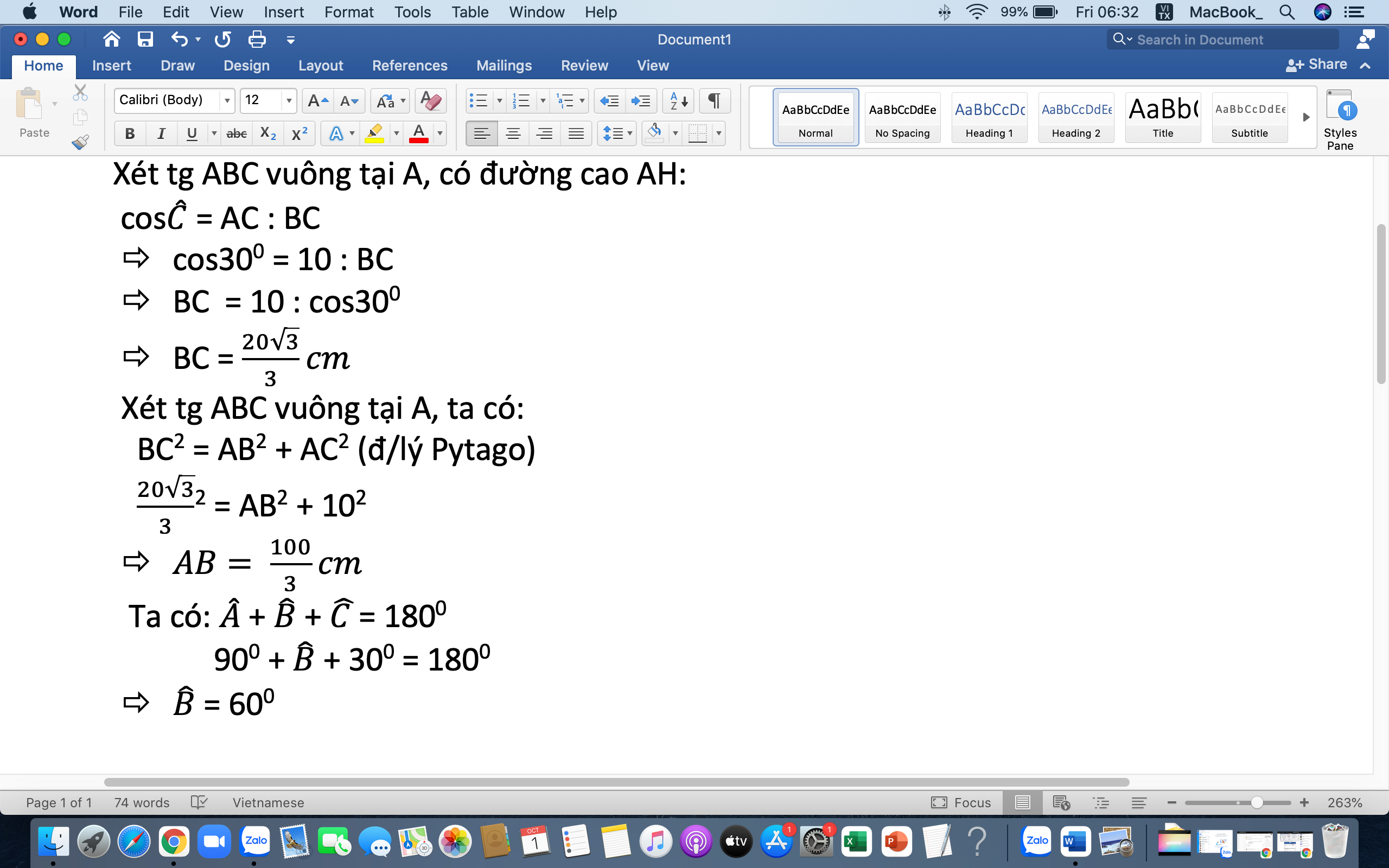
trong \(\Delta ABC\) vuông tại A
AB=AC.tanC=10.tan30=5,77
CB=\(\sqrt{AC^2+AB^2}=\sqrt{10^2+5,77^2}=11,55\)
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5,77.10}{11,55}=5\)
\(\widehat{B}=90-\widehat{C}=90-30=60\)
Đúng 1
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ AB. Vẽ AH vuông góc với CD. CMR: CH=\(\dfrac{CD+AB}{2}\). mn giúp mình vs ạ, mình đang cần gấp ạ. <33 Thanks mn nhiều.
Cho tam giác ABC cân tại A. Vẽ AH vuông góc với BC
a) cm tam giác AHB=tam giác AHC
b) Vẽ HM vuông góc với AB, HN vuông góc với AC. cm tam giác AMN cân
c) cm MN//BC
d) cm \(AH^2+BM^2=AN^2+BH^2\)
CHỈ CẦN GIUP MÌNH CÂU D THÔI CÁC BẠN NHÉ. CẢM ƠN TRƯỚC
KHÔNG CẦN VẼ HÌNH CŨNG ĐC
xet tg AMH vuong tai M co; AH2 = AM2 + HM2
tg BMH co; BM2 = BH2-HN2
cong 2 pt ban toi da nhan ra chua ban co thay AM=AN ; HM = HN thay vao ban se thay phep dieu ky
ma toi mang den cho ban la dpcm
Đúng 0
Bình luận (0)