Giải hệ phương trình:
\(x+y+z=12\)
\(ax+5y+4z=46\)
\(5x+ay+3z=38\)
a là tham số
Giải hệ phương trình: \(\hept{\begin{cases}x+y+z=12\\ax+5y+4z=46\\5x+ay+3z=38\end{cases}}\) (với a là tham số )
Giải hệ phương trình : \(\left\{{}\begin{matrix}x+y+z=12\\ãx+5y+4z=46\\5x+ay+3z=38\end{matrix}\right.\) (với a là tham số)
giải hệ pt 3 ẩn \(\int^{x+y+z=12}_{\int^{ax+5y+4z=46}_{5x+ay+3z=38}}\)
dùng máy tính giải hệ phương trình là ra kết quả x= 2/5 y=-2/5 z =12
e ko chắc lắm vì em ms lớp 8
eo lớp 8 bấm máy giỏi nhỉ nhưng có a bấm kiểu gì hả
Haha =)) V~ cả bấm máy luôn á ^^
Hên xui áp dụng phương pahsp thế đi ;P
x= 12-y-z
Thế vào may đâu ra :D
bài này làm sao vay?:
giải hệ pt: {x+y+z=12, ax+5y+4z=46, 5x+ay+3z=38}
Trong bài này a là tham số, nên nghiệm được tính theo a.
Từ pt thứ 1 --> x = 12 -y-z, thế giá trị x này vào 2 pt dưới (chịu khó biến đổi ) ta được:
(5-a)y +(4-a)z=46-12a. (1)
(a-5)y -2z = -22. (2)
Cộng lại hai vế của 2 pt trên ta được:
(2-a)z = 24 - 12a
<=> (2-a)z = 12(2-a)
=>z =12.(a khác 2)
Thế z vào pt(2) ta có y=2/(a-5).
Từ x=12 - y - z => x= -y= -2/(a-5).
Vậy x = -2/(a-5), y = 2/(a-5), z = 12 với a thuộc R, a khác 5 và khác 2.
Cho hệ phương trình 2 x - 3 y + 4 z = - 5 - 4 x + 5 y - z = 6 3 x + 4 y - 3 z = 7 . Giả sử (x;y;z) là nghiệm của hệ phương trình, khi đó x+y+z bằng
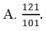
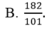
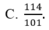
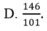
Giải hệ phương trình: \(\hept{\begin{cases}ax+y+z=a^2\\x+ay+z=3a\\x+y+az=2\end{cases}}\) ( a là tham số)
\(\hept{\begin{cases}ax+y+z=a^2\left(1\right)\\x+ay+z=3a\left(2\right)\\x+y+az=2\left(3\right)\end{cases}}\)
Lấy (1) + (2) + (3) vế theo vế được
\(\left(2+a\right)\left(x+y+z\right)=a^2+3a+2=\left(a+2\right)\left(a+1\right)\)
Với a = -2 thì
\(0.\left(x+y+z\right)=0\)bạn làm tiếp nhé
Với a # -2 thì
\(x+y+z=a+1\left(4\right)\)
Lấy (4) lần lược - cho (1), (2), (3) thì tìm được x,y,z
Giải hệ phương trình với a là tham số:
\(\hept{\begin{cases}ax+y+z=a^2\\x+ay+z=3a\\x+y+az=2\end{cases}}\)
Từ pt 1 ta có thể biến đổi : \(ax+y+z=a^2\)
\(< =>a=\frac{ax+y+z}{a}\)
\(< =>x+y+z=a\)
\(< =>3x+3y+3z=x+ay+z\)
\(< =>2x+y\left(3-a\right)+2z=0\)
\(< =>2a+y-ay=0\)
\(< =>2a+y-ay-2=-2\)
\(< =>a\left(2-y\right)-\left(2-y\right)=-2\)
\(< =>\left(a-1\right)\left(2-y\right)=2.\left(-1\right)=-1.2=-2.1=1.\left(-2\right)\)
\(< =>\left(a;y\right)=\left(3;3\right)=\left(0;0\right)=\left(-1;1\right)=\left(2;4\right)\)
Bạn thay vào là đc :)) giải sai hay đúng cg ko bt nx :(
GIẢI GIÚP MÌNH BÀI TOÁN NÀY ĐI Ạ!
Tìm nghiệm nguyên của hệ phương trình
\(\hept{\begin{cases}xy=x+y-z\\xz=2\left(x-y+z\right)\\yz=3\left(y-x+z\right)\end{cases}}\)
Tìm nghiệm nguyên dương của hệ phương trình
\(\hept{\begin{cases}x=5y+3\\x=11z+7\end{cases}}\)(x,y,z nhỏ nhất)
\(\hept{\begin{cases}x+2y+3z=20\\3x+5y+4z=37\end{cases}}\)(x,y,z nhỏ nhất)
4x-3y/10 =3z-5x/9=5y-4z/8
Và x+2y-z=12.Tìm x, y, z