Cho tam giác ABC có M,N,P lần lượt là trung điểm của AB, AC, BC.
d1, d2 lần lượt là đường trung trực của AB và AC.
Gọi E là giao điểm của d1 và d2.
Chứng minh EP là đường trung trực của BC
Vẽ ∆ A B C có AB < AC, vẽ M, N, E lần lượt là trung điểm của BC, AB, AC. Gọi d 1 , d 2 , d 3 lần lượt là ba đường trung trực của ba cạnh BC, AB, AC. Ghi đầy đủ kí hiệu lên hình vẽ và nêu nhận xét về giao điểm của ba đường thẳng trên
Ba đường thẳng cùng đi qua một điểm và điểm đó cách đều 3 đỉnh của tam giác (sẽ được chứng minh ở chương sau lớp 7)
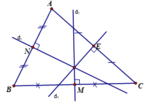
cho tam giác nhọn ABC.Kẻ d1 là đường trung trực của cạnh AB,d2 là đường trung trực của cạnh AC,gọi O là giao điểm của d1 và d2 lấy M là trung điểm của cạnh BC,dùng thước đo góc xác định số đo của OBM
Cho tam giác nhọn ABC. Kẻ là đường trung trực của cạnh AB, là đường trung trực của cạnh AC, gọi O là giao điểm của d 1 và d 2 . Lấy M là trung điểm của cạnh BC. Dùng thước đo góc xác định số đo của O M B ^ .
1) Cho tam giác ABC có AB < AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.
a/ chứng minh PN là đường trung trực của AH
b/ chứng minh tứ giác MNPH là hình thang
2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB = 60 độ. Gọi B' , C' lần lượt là hình chiếu của B, C trên AC và BD.
a/ Chứng minh A, B', C' = 1/2 BC
b/ gọi E là trung điểm BC, chứng minh tam giác EB'C' là tam giác đều
1) Cho tam giác ABC có AB < AC. Đường cao AH. Gọi M,N,P lần lượt là trung điểm của các cạnh BC, AC, AB.
a/ chứng minh PN là đường trung trực của AH
b/ chứng minh tứ giác MNPH là hình thang
2) cho hình thang cân ABCD. có AB // CD. I là giao điểm của 2 đường chéo AC và BC. góc AIB = 60 độ. Gọi B' , C' lần lượt là hình chiếu của B, C trên AC và BD.
a/ Chứng minh B', C' = 1/2 BC
b/ gọi E là trung điểm BC, chứng minh tam giác EB'C' là tam giác đều
Cho tam giác ABC vuông tại A gọi d, t lần lượt là đường trung trực của các đoạn thẳng AB và AC. Gọi E là giao điểm của đường thẳng d, t Chứng minh rằng E là trung điểm của BC.
E nằm trên đường trung trực của AB
=>EA=EB
E nằm trên đường trung trực của AC
=>EA=EC
=>EA=EB=EC
=>E là tâm đường tròn ngoại tiếp ΔABC(1)
Ta có: ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC(2)
Từ (1) và (2) suy ra E là trung điểm của BC
Cho tam giác ABC . Gọi I là giao điểm của các đường phân giác trong của các góc của tam giác . từ I kẻ IM vuông góc AB , IN vuông góc với BC , IK vuông góc với AC . Qua A kẻ đường thẳng d1 song song MN , d1 cắt đường thẳng NK tại E . Qua a kẻ đường thẳng d2 cắt MN tại D . Đường thẳng ED cắt AC , AB lần lượt tại B và Q . CHỨNG MINH P, Q là đường trung bình của tam giác ABC
1 like
cho tam giác ABC có góc A >90độ. Gọi d1,d2 lần lượt là các đường trung trực của AB,AC và chúng cắt nhau tại O,cắt BC theo thứ tự ở D và E,nối AD,AE,OB,OC.Tìm các tam giác bằng OAD,các tam giác bằng Tam giác OAE
Cho tứ giác ABCD có AC vuông góc BD. Gọi M, N lần lượt là trung điểm AB, AD. Qua M Vẽ đường thẳng d1 vuông góc CD. Qua N Vẽ đường thẳng d2 vuông góc BC. Chứng minh d1 và d2 và AC đồng quy
P/s làm ơn giúp em, cần ga61ppppppppppppppppppp!!!!!!!!!!!!!!!!!!!!!!!!!!