Bài 2: Hai đường thẳng vuông góc
Các câu hỏi tương tự
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB 4(cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD AB. Trên đường thẳng d lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD
a) Đo và cho biết số đo của góc ADC
b) Đo và cho biết số đo của góc BCD
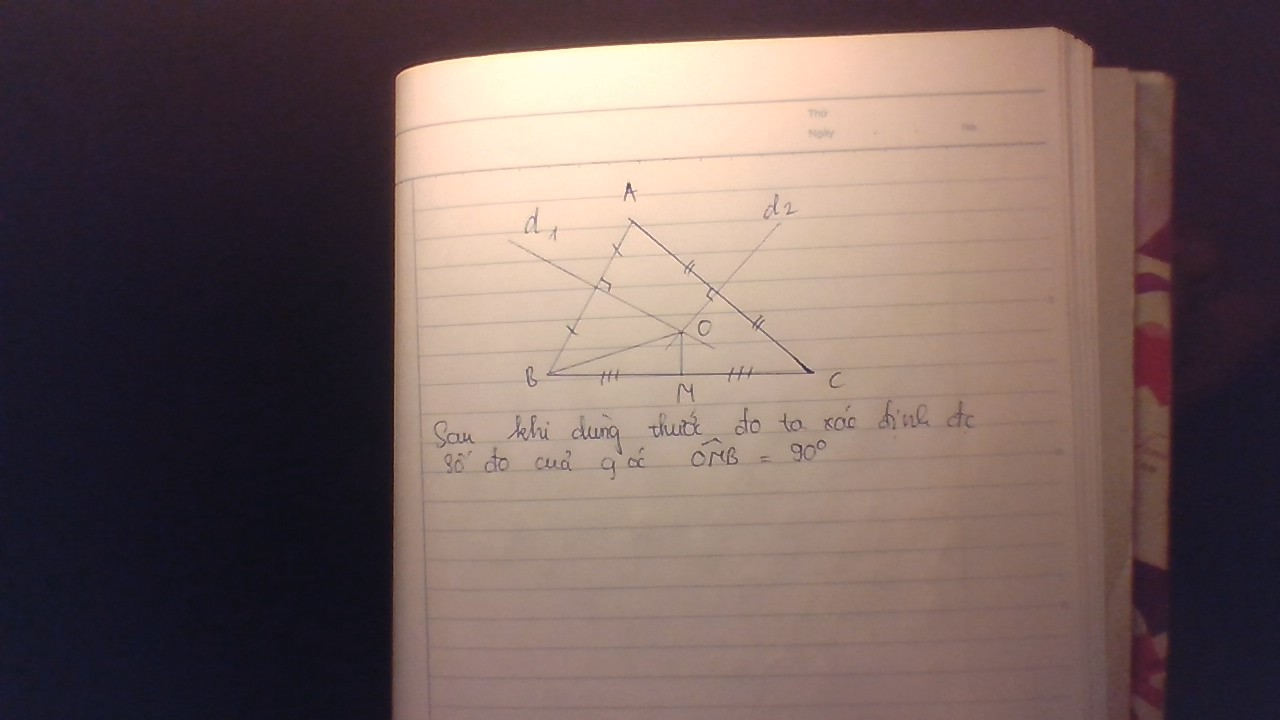
c) Đo và cho biết số đo của góc BOC
Đọc tiếp
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB = 4(cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d' đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD = AB. Trên đường thẳng d' lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC = AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD
a) Đo và cho biết số đo của góc ADC
b) Đo và cho biết số đo của góc BCD
c) Đo và cho biết số đo của góc BOC
: Vẽ hai đường thẳng aa’ và bb’ vuông góc với nhau tai M, trên đường thẳng aa’ lấy hai điểm AB sao cho M là trung điểm của AB. Ghi đầy đủ kí hiệu lên hình vẽ và chứng tỏ đường thẳng bb’ là đường trung trực của đoạn thẳng AB
Cho góc nhọn XoY gọi A là điểm bất kì nằm trong góc XoY . Ox, tại B qua A kẻ đường thẳng vuông góc với tia Oy tại C vẽ đường trung trực của BC
Cho tam giác nhọn ABC, M là trung điểm của BC. Đường vuông góc với AB tại B cắt đường thẳng AM tại D. Trên tia MA lấy điểm E sao cho ME = MD.
a,Chứng minh tam giác BMD = tam giác CME
b,chứng minh BD = EC
c,Chứng minh EC vuông góc với AB
Vẽ góc xOy=60 độ. Lấy A ∈ Ox rồi vẽ đường thẳng a ⊥Ox tại A. Lấy B∈Oy rồi vẽ đường thẳng b⊥Oy tại B. Gọi C là giao điểm của hai đường thẳng a và b. Vẽ đường trung trực của đoạn thẳng OC.
a) Vẽ tam giác ABC. Vẽ các đường trung trực của các đoạn thẳng AB, BC, CA
b) Vẽ đường tròn tâm O bán kính R = 3(cm). Lấy 3 điểm A, B, C phân biệt bất kì trên đường tròn. Vẽ các dây AB, BC, CA. Vẽ các đường trung trực của đoạn thẳng AB, BC, CA
cho đoạn thẳng AB = 4cm, I là trung điểm của AB. Vẽ đường trung trực của đoạn AB và tính đoạn IB.
Vẽ đoạn thẳng AB = 3cm, BC = 4cm. Vẽ đường trung trực của các đoạn thẳng AB, BC, AC trong các trường hợp sau:
a.A, B, C thẳng hàng sao cho B nằm giữa A và C.
b.A, B, C là 3 đỉnh của tam giác.
Cho ABC có AB = AC. Gọi M là trung điểm AC. Trên tia
đối của tia MB lấy điểm D sao cho MD = MB.
a) Chứng minh: ABM = CDM và AD // BC.
b) Gọi N là trung điểm của BC. Chứng minh: AN ⊥ AD.
c) Gọi P là trung điểm AD. Chứng minh: N, M, P thẳng hàng.