cho tam giác ABC các tia p/g của các góc B và C cắt nhau tại I.Qua I kẻ các đường thẳng song song vs BC cắt cạnh AB và AC thứ tự ở D và E.
a) kể tên các hình thang trong hình vẽ
b) c/m: BD + EC = DE
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
a) Tìm các hình thang trong hình vẽ
b)chứng minh rằng hình thang BDEC là một cạnh đáy bằng tổng hai cạnh bên
b: Xét ΔDBI có
\(\widehat{DBI}=\widehat{DIB}\)
nên ΔDBI cân tại D
Xét ΔEIC có \(\widehat{EIC}=\widehat{ECI}\)
nên ΔEIC cân tại E
Ta có: DE=DI+IE
nên DE=DB+EC
Vậy: BDEC là hình thang có một cạnh đáy bằng tổng hai cạnh bên
Cho tam giác ABC, các tia phân giác của góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt cạnh AB và AC tại D và E.
a) Vẽ hình và tìm các hình thang trong hình vẽ.
b) Chứng minh rằng hình thang BCED có một cạnh đáy bằng tổng hai cạnh bê
\(a,\) Các hình thang \(BDEC;BDIC;BIEC\)
\(b,DE//BC.nên.\widehat{B_1}=\widehat{I_1}\left(so.le.trong\right)\)
Mà \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right)\) nên \(\widehat{B_2}=\widehat{I_1}\Rightarrow\Delta DIB\) cân tại D
\(\Rightarrow DI=DB\left(1\right)\)
\(DE//BC.nên.\widehat{C_1}=\widehat{I_2}\left(so.le.trong\right)\)
Mà \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right)\) nên \(\widehat{C_2}=\widehat{I_2}\Rightarrow\Delta IEC\) cân tại E
\(\Rightarrow EI=EC\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow DI+IE=BD+EC\\ \Rightarrow DE=BD+CE\left(Đpcm\right)\)
Bài 2 Cho △ABC Các tia phân giác của B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB và AC ở D và E
a) Tìm các hình thang có trong hình? Vì sao?
b) CM: △ABDI và △IEC là tam giác cân.
c) CM: DE=BD+CE
a,
Do \(DE||BC\) (gt) \(\Rightarrow BDEC\) là hình thang
Do \(DE||BC\Rightarrow DI||BC\Rightarrow BDIC\) là hình thang
Do \(DE||BC\Rightarrow IE||BC\Rightarrow BIEC\) là hình thang
b.
Do \(DI||BC\Rightarrow\widehat{CBI}=\widehat{BID}\) (so le trong)
Mà \(\widehat{CBI}=\widehat{DBI}\) (do BI là phân giác góc B)
\(\Rightarrow\widehat{DBI}=\widehat{BID}\)
\(\Rightarrow\Delta BDI\) cân tại D
Tương tự ta có \(\widehat{ICB}=\widehat{CIE}\) (so le trong) và \(\widehat{ICB}=\widehat{ICE}\) (do IC là phân giác góc C)
\(\Rightarrow\widehat{CIE}=\widehat{ICE}\Rightarrow\Delta IEC\) cân tại E
c.
Từ câu b, do \(\Delta BDI\) cân \(\Rightarrow DB=DI\)
Do \(\Delta IEC\) cân \(\Rightarrow IE=CE\)
\(\Rightarrow BD+CE=DI+IE=DE\left(đpcm\right)\)
a,
Do (gt) là hình thang
Do là hình thang
Do là hình thang
b.
Do (so le trong)
Mà (do BI là phân giác góc B)
cân tại D
Tương tự ta có (so le trong) và (do IC là phân giác góc C)
cân tại E
c.
Từ câu b, do cân
Do cân
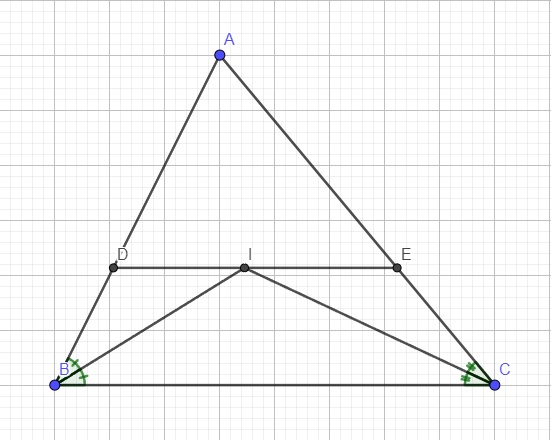
Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E. Tìm các hình thang trong hình vẽ.
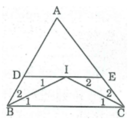
Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC
Cho tam giác ABC, các tia phân giác góc B, C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC cắt AB và AC lần lượt tại D và E.
a, Tìm các hình bình hành có trong hình.
b, Chứng minh rằng: tam giác BID cân ở D và tam giác IEC cân ở E.
c, So sánh DE với tổng BD+CE.
b) Ta có: \(\widehat{DBI}=\widehat{IBC}\)(gt)
mà \(\widehat{DIB}=\widehat{IBC}\)(hai góc so le trong, DI//BC)
nên \(\widehat{DBI}=\widehat{DIB}\)
hay ΔDIB cân tại D
Ta có: \(\widehat{EIC}=\widehat{ICB}\)(hai góc so le trong, IE//BC)
mà \(\widehat{ECI}=\widehat{ICB}\)(gt)
nên \(\widehat{EIC}=\widehat{ECI}\)
hay ΔEIC cân tại E
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I.
Qua I kẻ đường thẳng song song với AB cắt AC và BC ở D và E.
Chứng minh rằng DE = AD + BE
Giúp mình với, cảm ơn mn nhìu !!
Xét ΔDAI có góc DAI=góc DIA(=góc BAI)
nen ΔDAI cân tại D
=>DA=DI
Xét ΔEIB có góc EIB=góc EBI(=góc ABI)
nên ΔEIB cân tại E
=>EB=EI
DE=DI+IE
=>DE=EB+AD
cho tam giác ABC . các tia phân giác của góc B và góc C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC , cắt AB và AC theo thứ tự tại D và E . CMR :DE=BD+CE
Cho tam giác ABC,các tia phân giác của các góc B và C cắt nhau ở I.Qua I kẻ đường thẳng song song với BC.Gọi giao điểm của đường thẳng này với AB,AC theo thứ tự là D và E.Chứng minh rằng:DE=BD+CE
Vì CI là phân giác \(\widehat{C}\) (gt). \(\Rightarrow\) \(\widehat{ICB}=\widehat{ECI.}\)
Mà \(\widehat{EIC}=\widehat{ICB}\) \(\left(DE//BC\right).\)
\(\Rightarrow\) \(\widehat{ICB}=\widehat{ECI}=\widehat{EIC}.\)
Xét tam giác IEC: \(\widehat{ECI}=\widehat{EIC}\left(cmt\right).\)
\(\Rightarrow\) Tam giác IEC cân tại E. \(\Rightarrow\) \(EI=EC\) (Tính chất tam giác cân).
Ta có: \(\widehat{DIB}=\widehat{IBC}\left(DE//BC\right);\widehat{DBI}=\widehat{IBC}\) (BI là phân giác \(\widehat{B}\)).
\(\Rightarrow\) \(\widehat{DIB}=\widehat{IBC}=\widehat{DBI}.\)
Xét tam giác BDI: \(\widehat{DIB}=\widehat{DBI}\left(cmt\right).\)
\(\Rightarrow\) Tam giác BDI cân tại D. \(\Rightarrow DB=DI\) (Tính chất tam giác cân).
Ta có: \(DE=DI+EI.\)
Mà \(\left\{{}\begin{matrix}DI=DB\left(cmt\right).\\EI=EC\left(cmt\right).\end{matrix}\right.\)
\(\Rightarrow DE=DB+EC.\)
cho tam giác ABC các tia phân giác của góc B và góc C cắt nhau tại I qua I kẻ đg thẳng song song BC CẮT các cạnh AB và AC ở D và E a) tìm CÁC hình thang trong hình vẽ
b) cmr hình thang BDEC có 1 cạnh đáy = tổng 2 cạnh bên