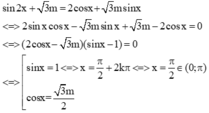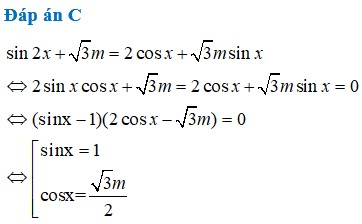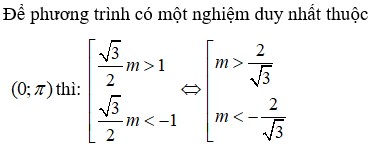Phương trình \(\sin2x=\frac{1}{2}\) có số nghiệm thuộc khoảng \(\left(0;2\pi\right)\) là:

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m để phương trình
2
.
sin
2
x
-
(
2
m
+
1
)
.
sin
x
+
2
m
-
1
0
có nghiệm thuộc khoảng
-
π...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 . sin 2 x - ( 2 m + 1 ) . sin x + 2 m - 1 = 0 có nghiệm thuộc khoảng - π 2 , 0 .
![]()
![]()
![]()
![]()
Phương trình
sin
2
x
−
2
2
có bao nhiêu nghiệm thuộc khoảng
0
;
π
? A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Phương trình sin 2 x = − 2 2 có bao nhiêu nghiệm thuộc khoảng 0 ; π ?
A. 4
B. 3
C. 2
D. 1
Đáp án C
PT 2 x = − π 4 + k 2 π 2 x = 5 π 4 + k 2 π ⇔ x = − π 8 + k π x = 5 π 8 + k π k ∈ ℤ
Vì x ∈ 0 ; π ⇒ 0 < − π 8 + k π < π 0 < 5 π 8 + k π < π ⇔ 1 8 < k < 9 8 − 5 8 < k < 3 8 ⇒ k = 1 k = 0 ⇒ x = 7 π 8 x = 5 π 8
Đúng 0
Bình luận (0)
Tìm số nghiệm thuộc khoảng - π ; π của phương trình cosx + sin2x = 0
A. 4
B. 3
C. 1
D. 2
Đáp án A
Ta có c o s x + sin 2 x = 0 ⇔ cos x + 2 sin x cos x = 0 ⇔ [ cos x = 0 sin x = - 1 2 ⇔ [ x = π 2 + k π x = - π 6 + k 2 π x = 7 π 6 + k 2 π
Mà x ∈ - π ; π ⇒ x ∈ - π 2 ; π 2 ; - π 6 ; - 5 π 6 .
Đúng 0
Bình luận (0)
Số nghiệm của phương trình sin 2 x + 2 sin x cos x + 3 cos 2 x = 3 thuộc khoảng (0; 2π) là:
A. 1
B. 2
C. 3
D. 4
Chọn C
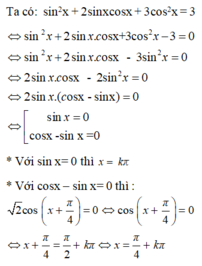
Vậy các nghiệm thuộc khoảng (0, 2π) là π 4 , π , 5 π 4
Đúng 0
Bình luận (0)
Phương trình
sin
2
x
−
π
4
sin
x
+
3
π
4
có tổng các nghiệm thuộc khoảng
0
;
π
bằng: A.
7
π
2
B....
Đọc tiếp
Phương trình sin 2 x − π 4 = sin x + 3 π 4 có tổng các nghiệm thuộc khoảng 0 ; π bằng:
A. 7 π 2
B. π
C. 3 π 2
D. π 4
Đáp án A
Ta có sin ( 2 x − π 4 ) = sin ( x + 3 π 4 )
⇔ 2 x − π 4 = x + 3 π 4 + k 2 π 2 x − π 4 = π − x − 3 π 4 + k 2 π ⇔ x = π + k 2 π 3 x = π 2 + k 2 π
⇔ x = π + k 2 π x = π 6 + k π 3
Vì nghiệm của phương trình thuộc 0 ; π nên ta có k =1
Do đó ⇔ x = π + 2 π x = π 6 + π 3 ⇔ x = 3 π x = π 2
Vậy tổng nghiệm của phương trình là 3 π + π 2 = 7 π 2
Đúng 0
Bình luận (0)
Số nghiệm của phương trình: \(sin2x+\sqrt{3}cos2x=\sqrt{3}\) trên khoảng \(\left(0;\dfrac{\pi}{2}\right)\)là bao nhiêu ?
Pt \(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(x\in\left(0;\dfrac{\pi}{2}\right)\)\(\Rightarrow\left[{}\begin{matrix}0< \dfrac{\pi}{6}+k\pi< \dfrac{\pi}{2}\\0< k\pi< \dfrac{\pi}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{6}< k< \dfrac{1}{3}\\0< k< \dfrac{1}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)\(\Leftrightarrow\left[{}\begin{matrix}k=0\\k\in\varnothing\end{matrix}\right.\)
Vậy có 1 nghiệm thỏa mãn
Đúng 4
Bình luận (0)
Tìm m để phương trình
sin
2
x
+
3
m
2
cos
x
+
3
m
sin
x
có duy nhất một nghiệm thuộc khoảng
0
;
π
A.
-
2
3
m
2
3
B....
Đọc tiếp
Tìm m để phương trình sin 2 x + 3 m = 2 cos x + 3 m sin x có duy nhất một nghiệm thuộc khoảng 0 ; π
A. - 2 3 < m < 2 3
B. - 2 3 ≤ m ≤ 2 3
C. m < - 2 3 ; m > 2 3
D. m ≤ - 2 3 ; m ≥ 2 3
Tìm m để phương trình
sin
2
x
+
3
m
2
cos
x
+
3
m
sin
x
có duy nhất một nghiệm thuộc khoảng
0
;
π
Đọc tiếp
Tìm m để phương trình sin 2 x + 3 m = 2 cos x + 3 m sin x có duy nhất một nghiệm thuộc khoảng 0 ; π
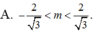
![]()
![]()
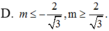
Tìm m để phương trình
sin
2
x
+
3
m
2
c
o
s
x
+
3
m
sin
x
có duy nhất một nghiệm thuộc khoảng
(
0
;
π
)
A.
-
2
3
m
2
3
B. ...
Đọc tiếp
Tìm m để phương trình sin 2 x + 3 m = 2 c o s x + 3 m sin x có duy nhất một nghiệm thuộc khoảng ( 0 ; π )
A. - 2 3 < m < 2 3
B. - 2 3 ≤ m ≤ 2 3
C. m < - 2 3 , m > 2 3
D. m ≤ - 2 3 , m ≤ 2 3