
giúp mình câu E,F,H
giúp mình câu d, e,f, h đi ạ, mình cảm ơn
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
Cho đoạn thẳng AB có C là trung điểm của đoạn thẳng đó.Gọi D là trung điểm của BC.Biết BD=3 cm
a) Vẽ hình và tính AB
b) Vẽ E nằm trên tia đối của AB.Lấy điểm F nằm giữa hai điểm A,E và điểm H nằm giữa hai điểm E,F sao cho HA >HE và cho biết HF=1/2(HA-HE).Chứng tỏ rằng F là trung điểm của AE
( Lưu ý: Bạn nào giải giúp mình thì xin vẽ giùm mình luôn cái hình.Không cần giải giúp mình câu a) mà giải giúp mình câu b).Thanks
GIÚP MÌNH CÂU E VÀ F VỚI 
k) Ta có: \(\dfrac{7}{20}+\dfrac{3}{5}+\dfrac{-1}{4}\)
\(=\dfrac{7}{20}+\dfrac{15}{20}+\dfrac{-5}{20}\)
\(=\dfrac{7+15-5}{20}\)
\(=\dfrac{17}{20}\)
làm giú mình câu H, E ,F
Chắc đề bài là xét tính liên tục của hàm số?
e.
\(\lim\limits_{x\rightarrow5}f\left(x\right)=\lim\limits_{x\rightarrow5}\dfrac{\sqrt[]{4x+16}+4-2x}{x^2-5x}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\left(\sqrt[]{4x+16}-6\right)+10-2x}{x^2-5x}=\lim\limits_{x\rightarrow5}\dfrac{\dfrac{\left(\sqrt[]{4x+16}-6\right)\left(\sqrt[]{4x+16}+6\right)}{\sqrt[]{4x+16}+6}-2\left(x-5\right)}{x\left(x-5\right)}\)
\(=\lim\limits_{x\rightarrow5}\dfrac{\dfrac{4\left(x-5\right)}{\sqrt[]{4x+16}+6}-2\left(x-5\right)}{x\left(x-5\right)}=\lim\limits_{x\rightarrow5}\dfrac{\dfrac{4}{\sqrt[]{4x+16}+6}-2}{x}\)
\(=\dfrac{\dfrac{4}{\sqrt[]{4.5+16}+6}-2}{5}=-\dfrac{1}{3}\)
\(f\left(5\right)=-\dfrac{1}{3}\)
\(\Rightarrow\lim\limits_{x\rightarrow5}f\left(x\right)=f\left(5\right)\)
Hàm liên tục tại \(x_0=5\)
f.
\(\lim\limits_{x\rightarrow-1}f\left(x\right)=\lim\limits_{x\rightarrow-1}\dfrac{x^3+x+2}{x^3+1}\)
\(=\lim\limits_{x\rightarrow-1}\dfrac{\left(x+1\right)\left(x^2-x+2\right)}{\left(x+1\right)\left(x^2-x+1\right)}=\lim\limits_{x\rightarrow-1}\dfrac{x^2-x+2}{x^2-x+1}\)
\(=\dfrac{1+1+2}{1+1+1}=\dfrac{4}{3}\)
Và \(f\left(-1\right)=\dfrac{4}{3}\)
\(\Rightarrow\lim\limits_{x\rightarrow-1}f\left(x\right)=f\left(-1\right)\)
Hàm liên tục tại \(x_0=-1\)
h.
\(\lim\limits_{x\rightarrow-3}f\left(x\right)=\lim\limits_{x\rightarrow-3}\dfrac{-2x^2-3x+9}{\sqrt{6-x}-3}\)
\(=\lim\limits_{x\rightarrow-3}\dfrac{\left(3-2x\right)\left(x+3\right)\left(\sqrt{6-x}+3\right)}{\left(\sqrt{6-x}-3\right)\left(\sqrt{6-x}+3\right)}\)
\(=\lim\limits_{x\rightarrow-3}\dfrac{\left(3-2x\right)\left(x+3\right)\left(\sqrt{6-x}+3\right)}{-\left(x+3\right)}\)
\(=\lim\limits_{x\rightarrow-3}\dfrac{\left(3-2x\right)\left(\sqrt{6-x}+3\right)}{-1}=-54\)
Và \(f\left(-3\right)=-54\)
\(\Rightarrow\lim\limits_{x\rightarrow-3}f\left(x\right)=f\left(-3\right)\)
Hàm liên tục tại \(x_0=-3\)
Giúp câu d . e . f . g . h
\(2,\\ a,x=36\Leftrightarrow P=\dfrac{6+1}{6-2}=\dfrac{7}{4}\\ b,x=6-2\sqrt{5}\Leftrightarrow\sqrt{x}=\sqrt{5}-1\\ \Leftrightarrow P=\dfrac{\sqrt{5}-1+1}{\sqrt{5}-1-2}=\dfrac{\sqrt{5}}{\sqrt{5}-3}=\dfrac{5-3\sqrt{5}}{2}\\ c,x=\dfrac{2}{2+\sqrt{3}}=4-2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{3}-1\\ \Leftrightarrow P=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-2}=\dfrac{\sqrt{3}}{\sqrt{3}-3}=\dfrac{3\left(\sqrt{3}+1\right)}{-6}=\dfrac{-\sqrt{3}-1}{2}\)
h: Ta có: \(x-7\sqrt{x}+10=0\)
nên x=25
Thay x=25 vào P, ta được:
\(P=\dfrac{5+1}{5-2}=\dfrac{6}{3}=2\)
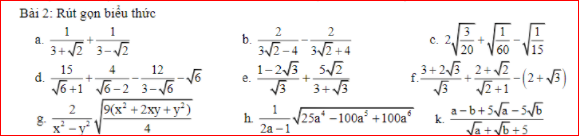
Giúp em câu e,f,g,h,k ạ
\(k,=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}\right)+5\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}+\sqrt{b}+5}\\ =\dfrac{\left(\sqrt{a}-\sqrt{b}\right)\left(\sqrt{a}+\sqrt{b}+5\right)}{\sqrt{a}+\sqrt{b}+5}=\sqrt{a}-\sqrt{b}\)
\(h,=\dfrac{1}{2a-1}\sqrt{25a^2\left(a^2-4a+4\right)}=\dfrac{1}{2a-1}\sqrt{25a^2\left(a-2\right)^2}\\ =\dfrac{\left|5a\left(a-2\right)\right|}{2a-1}=\left[{}\begin{matrix}\dfrac{5a\left(a-2\right)}{2a-1}\left(a\ge2;a\ne\dfrac{1}{2}\right)\\\dfrac{5a\left(2-a\right)}{2a-1}\left(0\le a< 2;a\ne\dfrac{1}{2}\right)\\\dfrac{-5a\left(2-a\right)}{2a-1}\left(a< 0\right)\end{matrix}\right.\)
Ai giúp mình câu này với:
Có 8 chữ cái từ A đến H. Mỗi một trong tám chữ cái đều khác nhau
số từ 1 đến 8.
A + B + C = F + G + H = 12. D + E = 12. C + D + E + F = 26. D = 5, H = 1. A, B,
và C là các con số. Tìm giá trị của mỗi chữ cái.
A,B,C,F,G,H,D,E
Dấu . là nhân nha
Giúp mình câu b c d e f k l m
giúp em câu e f g h đc ko ạ
e: vecto AM=(x-3;y+1)
vecto BM=(x+1;y-2)
vecto AC=(-2;0)
vecto AM=2*vecto BM-3*vecto AC
=>x-3=2*(x+1)+6 và y+1=2(y-2)
=>x-3=2x+8 và y+1=2y-4
=>x=-11 và y=5
f: Tọa độ H là:
\(\left\{{}\begin{matrix}x=\dfrac{3-1+1}{3}=1\\y=\dfrac{-1+2-1}{3}=0\end{matrix}\right.\)
g: K thuộc Oy nên K(0;y)
vecto AB=(-4;3)
vecto AK=(-3;y+1)
A,K,B thẳng hàng
=>\(-\dfrac{3}{-4}=\dfrac{y+1}{3}\)
=>y+1=9/4
=>y=5/4
h: P thuộc Ox nên P(x;0)
vecto PA=(x-3;1)
vecto PC=(x-1;1)
ΔPAC vuông tại P
=>vecto PA*vecto PC=0
=>(x-3)(x-1)+1=0
=>x^2-4x+3+1=0
=>x=2
=>P(2;0)