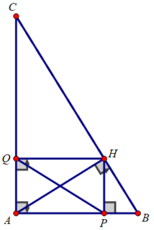
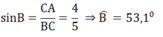Bài 10: Cho tam giác ABC vuông tại A có AB = 3cm, BC = 5cm, Đường cao AH.
a.Tính số đo góc B, C . Tính AH, AC ? b.Gọi AE là phân giác của góc A (E ![]() BC). Tính AE.
BC). Tính AE.
Bài 11: Cho ![]() ABC có BC = 12cm ; góc B = 600 ; góc C = 400
ABC có BC = 12cm ; góc B = 600 ; góc C = 400
a) Tính đường cao CH và cạnh AC ; b)Tính diện tích ![]() ABC(làm tròn đến chữ số thập phân thứ 2)
ABC(làm tròn đến chữ số thập phân thứ 2)