cho 2 số a,b thoã mãn\(\frac{a}{b}=\frac{-4}{5}\)và a2+2b2=16,5
giá trị lớn nhất của a+b là :
Những câu hỏi liên quan
Cho các số thực dương a,b,c thỏa mãn
f
a
b
+
b
c
+
c
a
+
3
+
f
2
-
2
a
2
-
2
b
2...
Đọc tiếp
Cho các số thực dương a,b,c thỏa mãn f a b + b c + c a + 3 + f 2 - 2 a 2 - 2 b 2 - 2 c 2 = 1 với hàm số f x = 4 x 4 x + 4 Giá trị lớn nhất của biểu thức P = a 2 + b 2 + c 2 - 1 a + b + c + 3 bằng
A. 17 6
B. 3
C. 13 6
D. 13 4
1/Số cặp số tự nhiên (a;b) thoã mãn : a/2+b/3=a+b/5
Số cặp số tự nhiên (x;y) thoã mãn \(\frac{3}{x}+\frac{y}{3}=\frac{5}{6}\)là......cặp
= 6 cặp
mk làm trong violympic rùi tin mk đi
Đúng 0
Bình luận (0)
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Đọc tiếp
cho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phươngcho a, b là hai số nguyên phân biệt lớn hơn 1 thỏa mãn a+2b2 - 2 là lũy thừa của một số nguyên tố khác 13, và b+2a2-2 chia hết cho a+2b2 - 2 chứng minh răng 2a+3 là số chính phương
Biết rằng tồn tại các số nguyên a, b sao cho hàm số
y
a
x
+
b
x
2
+
1
đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của
a
2
+
2
b...
Đọc tiếp
Biết rằng tồn tại các số nguyên a, b sao cho hàm số y = a x + b x 2 + 1 đạt giá trị nhỏ nhất, giá trị lớn nhất đều là các số nguyên và tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên. Giá trị của a 2 + 2 b 2 bằng
A. 36
B. 34
C. 41
D. 25
Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
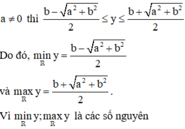
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
Đúng 0
Bình luận (0)
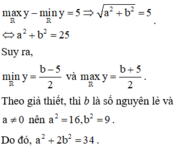
Cho các số thực dương a, b thỏa mãn \(1\le a\le2;1\le b\le2\). Tìm giá trị lớn nhất và giá trị nhỏ nhất của
P = \(a^2+b^2-\left(\frac{1}{a}+\frac{1}{b}\right)-4a-\frac{13b}{4}+4\)
Cho hai số thực a,b khác 0 thõa mãn \(2a^2+\frac{b^2}{4}+\frac{1}{a^2}=4\)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức S=ab+2019
\(2a^2+\frac{1}{a^2}+\frac{b^2}{4}=4\Leftrightarrow\left(a^2+\frac{1}{a^2}-2\right)+\left(a^2+\frac{b^2}{4}-ab\right)=4-ab-2\)
\(\Leftrightarrow\left(a-\frac{1}{a}\right)^2+\left(a-\frac{b}{2}\right)^2=2-ab\)
\(VF=2-ab=\left(a-\frac{1}{a}\right)^2+\left(b-\frac{b}{2}\right)^2\ge0\)
Hay \(ab\le2\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}a=\frac{1}{a}\\b=\frac{b}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(a;b\right)=\left(1;\frac{1}{2}\right)\\\left(a;b\right)=\left(-1;-\frac{1}{2}\right)\end{cases}}\)
Đúng 0
Bình luận (0)
ủa bạn tìm giá trị nhỏ nhất của biểu thức S=ab+2019 mà
Đúng 0
Bình luận (0)
cho a,b là các số nguyên dương thỏa mãn a2-ab+3/2b2 chia hết cho 25. Chứng minh rằng cả a và b đều chia hết cho 5.
Cho các số thực a,b,c thỏa mãn 5(a2+b2+c2)=6(ab+ac+bc). Tìm giá trị lớn nhất và nhỏ nhất của biểu thức P=(a+b+c)(\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\))
Cho ba số thực dương a, b, c thỏa mãn abc = 1. Tìm giá trị lớn nhất của:
\(A=\frac{1}{a^2+ab-a+5}+\frac{1}{b^2+bc-b+5}+\frac{1}{c^2+cb-c+5}\)
Ta có a2 + 1 \(\ge\)2a
Khi đó \(\frac{1}{a^2+ab-a+5}=\frac{1}{a^2+1+ab-a+4}\le\frac{1}{2a+ab-a+4}=\frac{1}{ab+a+4}\)
Tương tự ta được \(\frac{1}{b^2+bc-b+5}\le\frac{1}{bc+b+4};\frac{1}{c^2+ac-c+5}\le\frac{1}{ac+c+4}\)
Cộng vế với vế => A \(\le\frac{1}{ab+a+4}+\frac{1}{bc+b+4}+\frac{1}{ca+c+4}\)
=> 4A \(\le\frac{4}{ab+a+1+3}+\frac{4}{bc+b+1+3}+\frac{4}{ca+c+1+3}\)
\(\le\frac{1}{ab+a+1}+\frac{1}{3}+\frac{1}{bc+b+1}+\frac{1}{3}+\frac{1}{ac+a+1}+\frac{1}{3}\)
\(=\frac{1}{ab+a+1}+\frac{1}{bc+b+1}+\frac{1}{ac+a+1}+1\)
\(=\frac{1}{ab+a+1}+\frac{a}{abc+ab+a}+\frac{ab}{a^2bc+abc+ab}+1\)
\(=\frac{1}{ab+a+1}+\frac{a}{ab+a+1}+\frac{ab}{ab+a+1}+1=\frac{ab+a+1}{ab+a+1}+1=1+1=2\)
=> \(A\le\frac{1}{2}\)(Dấu "=" xảy ra <=> a = b = c = 1)
cho mik hỏi tí là làm sao ra được \(\frac{4}{ab+a+1+3}\le\frac{1}{ab+a+1}+\frac{1}{3}\) vậy ạ?
Dự đoán điểm rơi a = b = c = 1
Ta có : \(\frac{1}{ab+a+1}+\frac{1}{3}\ge\frac{\left(1+1\right)^2}{ab+a+1+3}\)(BĐT Schwarz)
\(=\frac{4}{a+b+c+4}\) (đpcm)