Cho tam giác ABC có BC=18cm, Gọi D, E lần lượt là trung điểm của AB và AC; M, N lần lượt là trung điểm của BD và CE. Tính MN?

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A (AB AC). Gọi D và E lần lượt là trung điểm của BC và AC. a) Chứng minh tứ giác ABDE là hình thang vuôngCho tam giác ABC vuông tại A (AB AC). Gọi D và E lần lượt là trung điểm của BC và ACa) Chứng minh tứ giác ABDE là hình thang vuôngb) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬTc) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Gọi D và E lần lượt là trung điểm của BC và AC. a) Chứng minh tứ giác ABDE là hình thang vuôngCho tam giác ABC vuông tại A (AB < AC). Gọi D và E lần lượt là trung điểm của BC và AC
a) Chứng minh tứ giác ABDE là hình thang vuông
b) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬT
c) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
a) Chứng minh tứ giác ABDE là hình thang vuông
b) Gọi K là điểm đối xứng của A qua D.CHỨNG MINH TỨ GIÁC ABKC LÀ HÌNH CHỮ NHẬT
c) Từ A kẻ AH vuông tại BC tại H.Gọi M là trung điểm BH.G là trung điểm của AH,F là trung điểm KC.chứng minh AM vuông góc MF toán 8
a: Xét ΔCAB có CE/CA=CD/CB
nên ED//AB và ED=AB/2
=>AEDB là hình thang
mà góc EAB=90 độ
nênAEDB là hình thang vuông
b: Xét tứ giác ABKC có
D là trung điểm chung của AK và BC
góc BAC=90 độ
Do đó: ABKC là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 16 cm. Gọi D và E lần lượt là trung điểm của AB và AC. Gọi M và N lần lượt là trung điểm của BD và EC. Tính MN?
A. 9cm
B. 8cm
C. 10cm
D. 12cm
* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
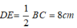
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB6m;AC8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 24HE mũ 2+4HD mũ 2
Đọc tiếp
Cho tam giác ABC vuông tại A, gọi M và E lần lượt là trung điểm của BC và AC, kẻ MD vuông góc với AB tại D
cho tam giác ABC vuông tại A,gọi M và E lần lượt là trung điểm của BC và AC,kẻ MD vuông góc với AB tại D.Gọi K là điểm đối xứng với M qua E
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a)biết AB=6m;AC=8cm.Tính BC;AM
b)chứng minh tứ giácADME là hình chữ nhật và tứ giác AMCK là hình thoi
c)kẻ MH vuông góc với AK(H thuộc AK).Chúng minh BC mũ 2=4HE mũ 2+4HD mũ 2
a:
Sửa đề: AB=6cm
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100=10^2\)
=>BC=10(cm)
ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(MA=MB=MC=\frac{BC}{2}=\frac{10}{2}=5\left(\operatorname{cm}\right)\)
b: Xét ΔABC có
M,E lần lượt là trung điểm của BC,CA
=>ME là đường trung bình của ΔABC
=>ME//AB
=>ME⊥AC tại E
Xét tứ giác ADME có \(\hat{ADM}=\hat{AEM}=\hat{DAE}=90^0\)
nên ADME là hình chữ nhật
Xét tứ giác AMCK có
E là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có MA=MC
nên AMCK là hình thoi
c: Gọi O là giao điểm của AM và DE
ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
=>O là trung điểm chung của AM và DE
ADME là hình chữ nhật
=>AM=DE
mà \(OA=OM=\frac{AM}{2};OD=OE=\frac{DE}{2}\)
nên \(OA=OM=OD=OE=\frac{AM}{2}=\frac{DE}{2}\)
ΔMHA vuông tại H
mà HO là đường trung tuyến
nên \(HO=\frac{MA}{2}\)
mà MA=DE
nên \(HO=\frac{DE}{2}\)
Xét ΔHDE có
HO là đường trung tuyến
\(HO=\frac{DE}{2}\)
Do đó: ΔHDE vuông tại H
=>\(HD^2+HE^2=ED^2\)
=>\(HD^2+HE^2=AM^2=\left(\frac12BC\right)^2=\frac14BC^2\)
=>\(BC^2=4\cdot HD^2+4\cdot HE^2\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có M, N, E lần lượt là trung điểm của BC, AC, AB. Gọi G là trọng tâm của tam giác ABC và D là trung điểm của MN. Chứng minh C, G, E, D thẳng hàng.
bạn tự vẽ hình nhé !
Nối EN, NM, ME. Ta có G là trọng tâm tam giác ABC nên G là giao điểm 3 đường trung tuyến , do đó E, G , C thẳng hàng.(1)
bây giờ chứng minh E,G,D thẳng hàng thì sẽ có C,G,E,D thẳng hàng.
Ta có E là trung điểm AB, N là trung điểm AC suy ra EN là đường trug bình tam giác ABC nên EN =1/2 BC và EN song2 với BC. lại có MC=1/2 BC ( M trug điểm BC)
suy ra EN = CM và EN song2 với CM từ đó ENCM là hình bình hành.
Xét hình bình hành ENCM có D là trung điểm MN suy ra D là trug điểm EC => ED=DC.
Vì G là trọng tâm tam giác ABC nên EG=1/3 EC=2/3ED (vì ED=1/2 EC)
Xét tam gác ENM có ED là trung tuyến , EG=2/3 ED suy ra G là trọng âm tam giác ENM. suy ra EGD thẳng hàng (2)
TỪ 1 và 2 suy ra E,G,D,C thẳng hàng
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC , các đường phân giác AD, BE lần lượt của góc A, góc B cắt nhau tại I. Gọi G là trọng tâm của tam giác ABC ( M là trung điểm của BC ).Có AB= 12cm, AC= 18cm, BC = 15cm.
Chứng minh IG//BC.
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB < AC , các đường phân giác AD, BE lần lượt của góc A, góc B cắt nhau tại I. Gọi G là trọng tâm của tam giác ABC ( M là trung điểm của BC ).Có AB= 12cm, AC= 18cm, BC = 15cm.
Chứng minh IG//BC.
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/2=CD/3=(BD+CD)/(2+3)=15/5=3
=>BD=6cm và CD=9cm
Xét ΔBAD có BI là phân giác
nên AI/ID=AB/BD=2
=>AI/AD=2/3=AG/AM
=>IG//BC
Đúng 0
Bình luận (0)
cho tam giác ABC có AB < AC . Trên AC lấy D sao cho AB = CD. Gọi E,F lần lượt là trung điểm của AD và BC . Gọi M là giao điểm của BA và FE. Chứng minh rằng tam giác AME cân.
ai đó giúp tui vs !!!!!!!!!!!!!!!!!!!!!
Đúng 0
Bình luận (0)
Cho tam giác ABC có BC = 14cm. Gọi D, E lần lượt là trung điểm của AB, AC. Tính DE?
Ta có :
D là trung điểm AB(gt)
E là trung điểm AC(gt)
=>DE//BC=>DE là đường trung bình của tam giác ABC=>DE=1/2 BC=> DE=14/2=7(cm)
Vậy DE=7cm
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC < BC), đường cao AH. Gọi D, E, F lần lượt là trung điểm của các cạnh AB, BC và AC. Gọi I là giao điểm của DF và AE.
b) Chứng I là trung điểm của DF.
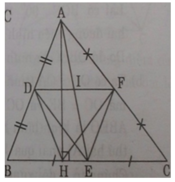
b) Ta có DF // BC (cmt) hay DI // BE; D là trung điểm của AD ⇒ I là trung điểm của AE và DI = BE/2
Trong ΔAEC có IF là đường trung bình nên IF = EC/2 mà EC = EB (gt) ⇒ IF = ID hay I là trung điểm của DF.
Đúng 0
Bình luận (0)













