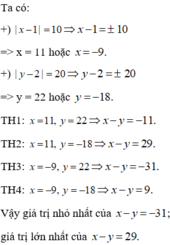cho x+y=2 tìm giá trị nhỏ nhất của x^2+y^2

Những câu hỏi liên quan
Cho x,y là các số thưc thỏa mãn x^2+y^2=x+y. Tìm giá trị nhỏ nhất, giá trị lớn nhất của A=x+y
\(x^2+y^2=x+y\\ \Leftrightarrow x^2-x+y^2-y=0\\ \Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\\ A=x+y=\left(x-\dfrac{1}{2}\right)+\left(y-\dfrac{1}{2}\right)+1\)
Áp dụng Bunhiacopski:
\(\left[\left(x-\dfrac{1}{2}\right)+\left(y-\dfrac{1}{2}\right)\right]^2\le\left(1^2+1^2\right)\left[\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2\right]=2\cdot\dfrac{1}{2}=1\\ \Leftrightarrow A\le1+1=2\)\(A_{max}=2\Leftrightarrow x=y=1\)
Đúng 2
Bình luận (1)
\(x^2+y^2\ge0\Rightarrow x+y=x^2+y^2\ge0\)
\(A_{min}=0\) khi \(x=y=0\)
Đúng 2
Bình luận (0)
Cách tìm max khác:
Ta có:
$(x-1)^2\geq 0, \forall x\in\mathbb{R}$
$\Rightarrow x^2+1\geq 2x$
Tương tự: $y^2+1\geq 2y$
$\Rightarrow 2(x+y)\leq x^2+y^2+2=x+y+2$
$\Rightarrow x+y\leq 2$ hay $A\leq 2$
Vậy $A_{\max}=2$ khi $x=y=1$
Đúng 1
Bình luận (0)
Cho x,y là các số thưc thỏa mãn x^2+y^2=x+y. Tìm giá trị nhỏ nhất, giá trị lớn nhất của A=x-y
Cho x,y thõa x^2+y^2-xy=1. Tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P=x^4+y^4-x^2y^2.
Từ gt ta có x^2+y^^2=xy+1
=>P=(x^2+y^2)^2-2x^2y^2-x^2y^2
=(xy+1)2-2x2y2-x2y2
=x2y2+xy+1-3x2y2=-2x2y2+xy+1
=......
Đúng 0
Bình luận (0)
\(1=x^2+y^2-xy\ge2xy-xy=xy\Rightarrow xy\le1\)
\(1=x^2+y^2-xy\ge-2xy-xy=-3xy\Rightarrow xy\ge-\dfrac{1}{3}\)
\(\Rightarrow-\dfrac{1}{3}\le xy\le1\)
\(P=\left(x^2+y^2\right)^2-2\left(xy\right)^2-\left(xy\right)^2=\left(xy+1\right)^2-3\left(xy\right)^2=-2\left(xy\right)^2+2xy+1\)
Đặt \(xy=t\in\left[-\dfrac{1}{3};1\right]\)
\(P=f\left(t\right)=-2t^2+2t+1\)
\(f'\left(t\right)=-4t+2=0\Rightarrow t=\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{3}\right)=\dfrac{1}{9}\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{3}{2}\) ; \(f\left(1\right)=1\)
\(\Rightarrow P_{max}=\dfrac{3}{2}\) ; \(P_{min}=\dfrac{1}{9}\)
Đúng 0
Bình luận (0)
Cho |x-1| = 10, |y-2| = 20. Tìm giá trị nhỏ nhất và giá trị lớn nhất của x - y.
cho x2+y2-xy=x+y. tìm giá trị lớn nhất , giá trị nhỏ nhất của biểu thucA=x^3+y^3
cho x,y>0 thỏa mãn x+y=1.tìm giá trị lớn nhất,giá trị nhỏ nhất của các biểu thức: A= 1/x^2+y^2 +1/xy,B= 1/x^2+y^2+3/4xy
có: \(\dfrac{1}{x^2+y^2}=\dfrac{1}{\left(x+y\right)^2-2xy}=\dfrac{1}{1-2xy}\)(1)
có \(\dfrac{1}{xy}=\dfrac{2}{2xy}\left(2\right)\)
từ(1)(2)=>A=\(\dfrac{1}{1-2xy}+\dfrac{2}{2xy}\ge\dfrac{\left(1+\sqrt{2}\right)^2}{1}=\left(1+\sqrt{2}\right)^2\)
=>Min A=(1+\(\sqrt{2}\))^2
Đúng 2
Bình luận (1)
b, ta có : \(x+y=1=>2x+2y=2\)
\(B=\dfrac{1}{x^2+y^2}+\dfrac{3}{4xy}=\dfrac{4}{4x^2+4y^2}+\dfrac{6}{8xy}\)\(\ge\dfrac{\left(2+\sqrt{6}\right)^2}{\left(2x+2y\right)^2}\)
\(=\dfrac{\left(2+\sqrt{6}\right)^2}{2^2}=\dfrac{5+2\sqrt{6}}{2}\)=>\(B\ge\dfrac{5+2\sqrt{6}}{2}\)
=>\(MinB=\dfrac{5+2\sqrt{6}}{2}\)
Đúng 0
Bình luận (0)
cho 2 số x,y thỏa mãn điều kiện:(x^2-y^2+1)^2+4x^2y^2-x^2-y^2=0.Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức x^2+y^2
1.
x thuộc {-3;-2;-1;0;1;...10} và y thuộc {-90;-89;-88;...;-1;0;1}
tìm giá trị lớn nhất và giá trị nhỏ nhất của x-y
2.
cho x thuộc {-2;-1;0;1;...;8} và y thuộc {-90;-89;-88;...;-1;0;1;2}
tìm giá trị lớn nhất và giá trị nhỏ nhất của x-y
cho x, y > 0 thoả x+y=2. tìm giá trị nhỏ nhất của B = \(^{x^2+y^2+\dfrac{1}{x^2+y^2}}\)
Ta có \(p=x^2+y^2\ge\dfrac{\left(x+y\right)^2}{2}=2\). Ta đi tìm GTNN của \(B=p+\dfrac{1}{p}\).
Do \(B=\dfrac{p}{4}+\dfrac{1}{p}+\dfrac{3p}{4}\) \(\ge2\sqrt{\dfrac{p}{4}.\dfrac{1}{p}}+\dfrac{3.2}{4}\) \(=\dfrac{5}{2}\). ĐTXR \(\Leftrightarrow\left\{{}\begin{matrix}x=y\\p=2\end{matrix}\right.\) \(\Leftrightarrow x=y=1\).
Vậy GTNN của B là \(\dfrac{5}{2}\) khi \(x=y=1\)
Đúng 4
Bình luận (0)