chứng minh rằng đường thẳng Mu song song với đường thẳng Tz 150 120 z T N M u
Đọc tiếp
chứng minh rằng đường thẳng Mu song song với đường thẳng Tz
Những câu hỏi liên quan
Cho hình bs 12
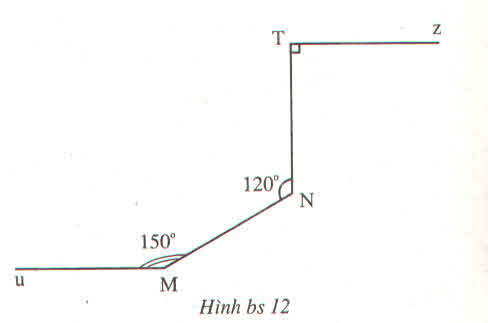
Chứng minh rằng đường thẳng Mu song song với đường thẳng Tz ?
chứng minh rằng đường thẳng Mu //với đường thẳng Z biết NMu=150,MNT=120,NTz=90
Cho hình bs 12
Chứng minh rằng đường thẳng Mu song song với đường thẳng Tz
Mỗi bài từ số I.4 đến số I.10 sau đây đều có bốn lựa chọn là (A), (B), (C) và (D) nhưng chỉ có một trong số đó là đúng. Hãy chọn phương án đúng.
Bài này có nhiều cách giải, ta có thể làm theo cách sau đây.
Từ điểm M vẽ đường thẳng Mn song song với đường thẳng TN.
+) Khi đó, vì ∠TNM + ∠NMn = 180° (hai góc trong cùng phía)
Mà ∠TNM = 120° nên ∠NMn = 60°.
+) Vẽ Mu’ là tia đối của Mu, biết ∠uMN = 150° nên tính được ∠NMu' = 30°.
Vì ∠uMN + ∠NMu’ = 180° (hai góc kề bù) biết ∠uMN = 150° nên tính được ∠NMu' = 30°.
Từ đó ∠nMu' = ∠NMn + ∠NMu' = 60° + 30° = 90°, tức là đường thẳng Mn vuông góc với đường thẳng Mu.
Do đường thẳng Mn song song với đường thẳng TN nên suy ra đường thẳng TN cũng vuông góc với đường thẳng Mu.
Từ đó Tz song song với Mu vì cùng vuông góc với TN.
Đúng 0
Bình luận (0)
a) Chứng minh rằng hai tia phân giác của hai góc nhọn hoặc hai góc tù có hai cặp cạnh tương ứng song song thì chúng song song với nhau.
b) Cho đường thẳng m vuông góc với đường thẳng n, đường thẳng p không vuông góc với n. Chứng minh p cắt n.
Dzaaa giúp emm vứi
bài 1: Chứng Minh rằng :
AB song song với DM song song với CD
biết góc A = C =120 độ
*đường thẳng OM nằm giữa đường thẳng AB và CD
điểm O nối với điểm A , điểm O nối với điểm C *
qua điểm O nằm trong tam giác ABC kẻ đường thẳng song song với AB cắt AC và BC ở D và E , kẻ đường thẳng song song với AC cắt AB và BC ở F và K , kẻ đường thẳng song song với BC cắt AB và AC ở M và N
chứng minh rằng \(\frac{AF}{AB}+\frac{BE}{BC}+\frac{CN}{CA}=1\)
Cho hình thang ABCD, đáy AB. Từ đỉnh C, kẻ đường thẳng song song với AD, đường này cắt BD tại P và cắt AB tại E. Qua D, kẻ đường thẳng song song với BC, đường này cắt AC tại N và AB tại F. Đường thẳng qua E, song song với AC cắt BC tại Q và đường thẳng qua F song song với BD cắt AD tại Ma, Chứng minh bốn điểm M,N,P,Q nằm trên 1 đường thẳng song song với hai đáyb, Chứng minh: MN PQc, Cho ABa, CDb. Chứng minh rằng các điểm M, N,P, Q theo thứ tự chia các đoạn thẳng AD, AC, BD, DC theo cùng 1 tỉ số...
Đọc tiếp
Cho hình thang ABCD, đáy AB. Từ đỉnh C, kẻ đường thẳng song song với AD, đường này cắt BD tại P và cắt AB tại E. Qua D, kẻ đường thẳng song song với BC, đường này cắt AC tại N và AB tại F. Đường thẳng qua E, song song với AC cắt BC tại Q và đường thẳng qua F song song với BD cắt AD tại M
a, Chứng minh bốn điểm M,N,P,Q nằm trên 1 đường thẳng song song với hai đáy
b, Chứng minh: MN = PQ
c, Cho AB=a, CD=b. Chứng minh rằng các điểm M, N,P, Q theo thứ tự chia các đoạn thẳng AD, AC, BD, DC theo cùng 1 tỉ số k. Tính k theo a và b.
Giải mục 1 trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
16 tháng 7 2023 lúc 8:48
Trong không gian, cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m; n lần lượt song song với hai đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD)
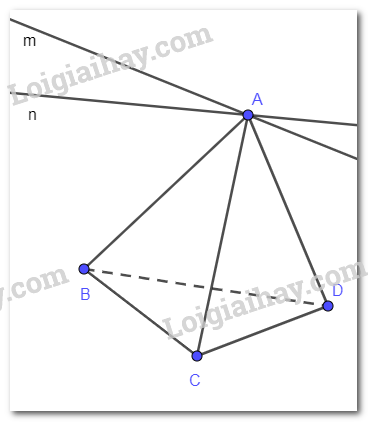
Ta có: m // BC suy ra m // (BCD).
n // BD suy ra n // (BCD).
Mặt phẳng (m,n) chứa hai đường thẳng cắt nhau m và n cùng song song với mặt phẳng (BCD) nên mặt phẳng (m, n) song song với mặt phẳng (BCD).
Đúng 0
Bình luận (0)
Cho điểm E thuộc cạnh AC của tam giác ABC.Qua B kẻ một đường thẳng I. Đường thẳng qua E và song song với BC cắt I tại N. Đường thẳng qua E và song song với AB cắt I tại M. Chứng minh rằng AN//MC
Cho tam giác ABC, một đường thẳng song song với BC cắt cạnh AB, AC lần lượt tại M và N. Qua C kẻ đường thẳng song song với BN cắt đường thẳng AB tại P. Chứng minh rằng: AB2 = AM . AP
Bài làm
Xét tam giác ABC có
MN // BC
Theo định lí Thales đảo có:
AM/AB = AN/AC. (1)
Xét tam giác APC có
BN // PC
Theo định lí Thales đảo có:
AB/AP = AN/AC. (2)
Từ (1) và (2) => AM/AB = AB/AP => AB² = AM . AP ( đpcm )