cho tam giác ABC cân AB=AC=10cm ; BC=16cm, đường cao AH , gọi I thuộc AH , AI =1/3 AH . Vẽ Cx // AH ,Cx giao BI tại D .
a) Tính các góc của tam giác ABC .
b) Tính diện tích của tam giác ABC
Những câu hỏi liên quan
cho tam giác abc cân tại a có ab=ac=10cm bc=8cm gọi g là trọng tâm của tam giác abc tính ag,bg,cg
Xem chi tiết
Cho tam giác ABC cân tại A có AB AC 13cm; BC 10cm. Tính sin A A. sin A
120
169
B. sin A
60
169
C. sin A
5
6
D. sin A
10
13
Đọc tiếp
Cho tam giác ABC cân tại A có AB = AC = 13cm; BC = 10cm. Tính sin A
A. sin A = 120 169
B. sin A = 60 169
C. sin A = 5 6
D. sin A = 10 13
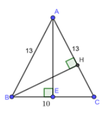
Vì tam giác ABC cân tại A nên AE là đường cao đồng thời là đường trung tuyến
=> E là trung điểm BC => EB = EC = 5
Xét ABE vuông tại E có:
Mặt khác:
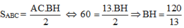
Xét ABH vuông tại H có:
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho tam giác ABC, biết.
AB=10cm; BC=26cm;ac=24cm
a)C/m tam giác ABC vuông
b)Trên tia đối tia AB lấy D sao cho AB=AD.C/m CA là tia phân giác DCB
c)C/m tam giác CDB cân 
a: Xét ΔACB có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
Do đó: ΔCAB=ΔCAD
Suy ra: \(\widehat{BCA}=\widehat{DCA}\)
hay CA là tia phân giác của góc BCD
c: Xét ΔCDB có CD=CB
nên ΔCDB cân tại C
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông cân tại A coa AB = AC = 10cm. Tam giác
vuông cân DEF nội tiếp tam giác ABC sao cho D,E,F lân lượt thuộc các cạnh
AB, BC, CA. Hãy xác định vị trí điểm D trên cạnh AB sao cho diện tích tam
giác DEF nhỏ nhất.
Cho tam giác ABC cân tại A. Vẽ trung tuyến AM của tam giác. Biết B C = 12 c m , A B = A C = 10 c m thì độ dài AM là:
A. 22cm
B. 4cm
C. 8cm
D. 10cm
Tam giác ABC cân tại A, AM là đường trung tuyến đồng thời là đường cao.
Có BM = BC/2 = 6cm
Áp dụng định lí Pytago trong tam giác vuông ABM có:
AM2 = AB2 - BM2 = 102 - 62 = 64 ⇒ AM = 8m. Chọn C
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A có AB = AC =13cm ; BC =10cm. Tính cos A
kẽ đường cao AH,tam giác ABC cân tại A=>AH cũng là trung tuyến của BC=>BH=1/2BC=5cm
xét tam giác AHB theo DL Pitago ta tính dc AH=12cm
=>cosBAH=AH/AB=12/13
=>cosBAC=2*12/13=24/13(vì AH là fân giác góc BAC)
Đúng 0
Bình luận (0)
1) Cho tam giác ABC cân tại A có AH là đường cao
a) Biết AB=8cm, BC=4cm. Tính diện tích tam giác ABC
b) Gọi N là trung điểm của AC. Tứ giác ANHB là hình gì?
2) Cho tam giác ABC cân tại A
a) Biết AB=10cm, BC=5cm. Đường trung tuyến AH. Tính diện tích tam giác ABC
b) Gọi M, N lần lượt là trung điểm của AB,AC. Tứ giác BMNC là hình gì?
Mn giúp mik vs bài này mik cần gấp!
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Đúng 1
Bình luận (0)
Cho tam giác cân ABC có AB=AC=10cm , BC=12cm . Gọi I là giao điểm các đường phân giác của tam giác . Tính độ dài BI
Lời giải:
Tam giác ABC cân tại A nên đường phân giác AH đồng thời là đường trung trực của BC
Áp dụng định lý pitago ta được:
\(AH^2=AB^2-BH^2=10^2-6^264\Rightarrow AH=8\)
Áp dụng tính chất đường phân giác ta được:
Đúng 0
Bình luận (0)
Bài 3. (3 điểm) Cho tam giác ABC cân, biết AB = 10cm, BC = 5cm có độ dài 3 cạnh của
tam giác là 3 số nguyên dương.
a) Tính độ dài cạnh AC và chứng minh rằng tam giác ABC cân tại A.
b) Gọi M, N lần lượt là trung điểm của AB và AC. Chứng minh ABN ACM
c) Chứng minh AB+BC>BN+CM
a: AB+BC>AC>AB-BC
=>15>AC>5
=>AC=10(cm)
=>ΔABC cân tại A
b: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM
Đúng 1
Bình luận (0)
cho tam giác ABC cân tại A biết AB=15cm.BC=10cm,phân giác góc B cắt AC tại D.
a) tính AD,CD
b)tính tỉ số diện tích tam giác ABD và tam giác BCD.
https://hoc24.vn/cau-hoi/.4762222558882
-Bạn chỉ cần thay đổi một chút thôi.
Đúng 1
Bình luận (0)