cho tam giác ABC có AB=AC, lấy điểm D\(\in\) AB,lấy điểm E \(\in\) AC sao cho AD=AE.gọi K là giao điểm của BE và CD. chứng minh:AK là tia p/g của góc A.
Những câu hỏi liên quan
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE.Gọi O là giao điểm của BE và CD. Chứng minh AO là tia phân giác của góc A
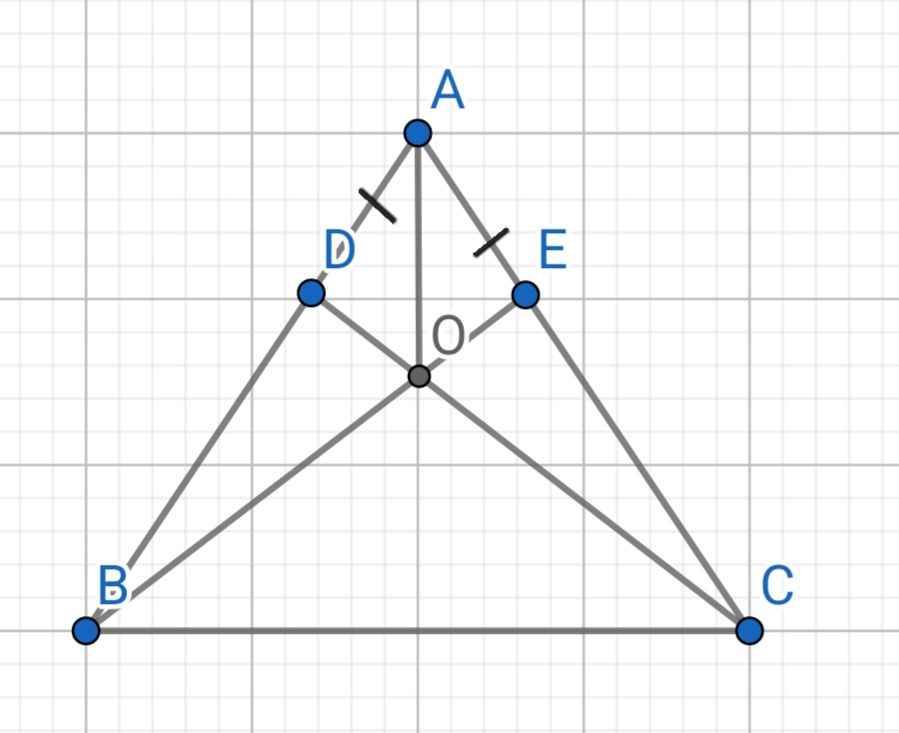∆ABC có:
AB = AC (gt)
⇒ ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
⇒ ∠DBC = ∠ECB
Do AB = AC (gt)
AD = AE (gt)
⇒ BD = AB - AD = AC - AE = CE
Xét ∆DBC và ∆ECB có:
DB = EC (cmt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆DBC = ∆ECB (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)
⇒ ∠BDO = ∠CEO
Do ∆DBC = ∆ECB (cmt)
⇒ ∠BCD = ∠CBE (hai góc tương ứng)
Mà ∠ACB = ∠ABC (cmt)
⇒ ∠ECO = ∠ACB - ∠BCD
= ∠ABC - ∠CBE
= ∠DBO
Xét ∆BOD và ∆COE có:
∠DBO = ∠ECO (cmt)
BD = CE (cmt)
∠BDO = ∠CEO (cmt)
⇒ ∆BOD = ∆COE (g-c-g)
⇒ OD = OE (hai cạnh tương ứng)
Xét ∆ADO và ∆AEO có:
AD = AE (gt)
AO là cạnh chung
OD = OE (cmt)
∆ADO = ∆AEO (c-c-c)
⇒ ∠DAO = ∠EAO (hai góc tương ứng)
⇒ AO là tia phân giác của ∠DAE
Hay AO là tia phân giác của ∠BAC
Đúng 0
Bình luận (0)
Cho tam giác ABC, AB=AC.trên cạnh AB lấy điểm D,trên cạnh AC lấy điểm E sao cho AD=AE.Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE=CD
b)△BMD=△CME
c)AM là tia phân giác của góc BAC
huhu giúp mình với ạ,mình cần giải gấp
a)Xét ΔABE và ΔACD có:
AB=AC(GT)
góc BAC chung
AE=AD(GT)
=>ΔABE=ΔACD(C.G.C)
⇒BE=CD(2 CẠNH TƯƠNG ỨNG)
góc ABE= góc ACD( 2 góc tướng ứng)
b)Có:AB=AC(GT)
Mà:AD=AE(GT)
=>AB-AD = AC-AE
=>BD=CE
Xét ΔBMD và ΔCME có:
góc ABE= góc ACD(CMT)
BD=CE(CMT)
góc BMD=CME(2 góc đối đỉnh)
=>ΔBMD=ΔCME(ch-gn)
=>BM=CM(2 cạnh tương ứng)
c)Xét ΔBAM và ΔCAM có:
AB=AC(GT)
AM chung
BM=CM(CMT)
=>ΔBAM=ΔCAM(c.c.c)
=>góc BAM= góc CAM(2 góc tướng ứng)
=>AM là tia phân giác góc BAC(ĐPCM)
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB=BC . Trên các cạnh AB và AC lấy điểm D và E sao cho AD=AE.Gọi K là giao điểm của BE và CD
Cho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho AD AE. Gọi K là giao điểm của CD và BECho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho ADAE.Gọi K là giao điểm của CD và BE.a,Cm: tam giác ADC tam giác AEBb,Cm:tam giác KBC cânc,trên tia đối của tia CB lấy điểm M sao cho CMCBTính góc ABC nếu BAC2*góc MAC
Đọc tiếp
Cho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho AD = AE. Gọi K là giao điểm của CD và BE
Cho tam giác ABC cân tại A,trên cạnh AB và AC lần lượt lấy điểm D và E sao cho AD=AE.Gọi K là giao điểm của CD và BE.
a,Cm: tam giác ADC= tam giác AEB
b,Cm:tam giác KBC cân
c,trên tia đối của tia CB lấy điểm M sao cho CM=CB
Tính góc ABC nếu BAC=2*góc MAC
a: Xét ΔADC và ΔAEB có
AD=AE
góc DAC chung
AC=AB
=>ΔADC=ΔAEB
b: AD+DB=AB
AE+EC=AC
mà AB=AC và AD=AE
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
góc DBC=góc ECB
BC chung
=>ΔDBC=ΔECB
=>góc KBC=góc KCB
=>ΔKBC cân tại K
Đúng 1
Bình luận (1)
Cho tam giác ABC,AB=AC.Trên cạnh AB lấy điểm D,trên cạnh AC lấy điểm E sao cho AD=AE.Gọi M là giao điểm của BE và CD.Cm
a)BE=CD
b)Tam giác BMD =tam giác CME
c)AM là tia phân giác của góc BAC
cho tam giác abc có ab=ac.trên cạnh ab à ac lấy diểm d và e sao cho ad=ae.gọi k là giao điểm của be và cd.cmr
a,be=cd
b, tam giác kbd= tam giác kce
a) Ta có:
ABC cân tại A nên gócABC= góc ACB và AB=AC
AB=AC (2 cạnh tương ứng)
AD+BD=AE+CE
Mà AD=AE
SUY RA:BD=CE
Xét tam giác bcd và tam giác ceb có
góc ABC= GÓC ACB(CMT)
BD=CE(CMT)
BCchung
do đó tam giác bcd= tam giác ceb(c.g.c)
suy ra BE=CD(đpcm)
Vậy ......
chúc bạn học tốt
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE a) Chứng minh rằng BE = CD b) Gọi O là giao điểm của BE và CD, chứng minh ao là tia phân giác của góc bac
a: Xét ΔABE và ΔACD có
AB=AC
\(\stackrel\frown{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
Đúng 0
Bình luận (0)
cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, lấy điểm E trên cạnh AC sao cho AD=AE
a) Chứng minh : BE = CD
b) Gọi O là giao điểm của BE và CD. Chứng minh rằng ΔBOD = ΔCOE
c) Chứng minh: AO là tia phân giác của góc BAC
cho tam giác ABC có AB = AC . Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh rằng :
a, BE = CD
b, MDB = MEC
c, Am là p/g của góc BAC
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
Đúng 1
Bình luận (0)