tính các cạnh còn lại

Những câu hỏi liên quan
Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng:
A. 45
B. 60
C. 55
D. 35
Tam giác thứ nhất có các cạnh là 12 < x < y
Tam giác thứ hai có các cạnh là x < y < 40,5
Vì hai tam giác đồng dạng nên 12 x = x y = y 40 , 5 ta có x.y = 12.40,5 và x 2 = 12 y .
Do đó x 2 = 12 y = 12 . 12.40 , 5 x nên x 3 = 12 . 12 . 40 , 5 = 18 3 suy ra x = 18
Suy ra y = 12.40 , 5 18 = 27
Vậy x = 18, y = 27 => S = 18 + 27 = 45
Đáp án: A
Đúng 0
Bình luận (0)
Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
A. x = 5; y = 10
B. x = 6; y = 12
C. x = 12; y = 18
D. x = 6; y = 18
Tam giác thứ nhất có các cạnh là 8 < x < y
Tam giác thứ hai có các cạnh là x < y < 27
Vì hai tam giác đồng dạng nên 8 x = x y = y 27 ta có x.y = 8.27 và x 2 = 8 y .
Do đó x 2 = 8 y = 8 . 8.27 x nên x 3 = 64 . 27 = ( 4 . 3 ) 3
Vậy x = 12, y = 18
Đáp án: C
Đúng 0
Bình luận (0)
cho hình chóp SABC có SA=x và SB=y. các cạnh còn lại đều bằng 1. tính thể tích hình chóp theo x và y làm theo 2 cách
Lần lượt tính độ dài các cạnh huyền \(a\), \(b\), \(c\), \(d\) của các tam giác vuông trong Hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại.
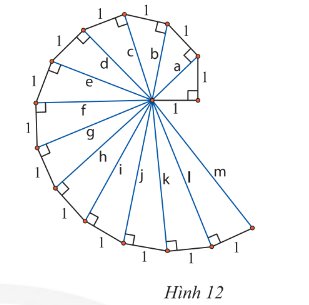
a=căn 1^2+1^2=căn 2(cm)
b=căn a^2+1^2=căn 3(cm)
c=căn (căn 3)^2+1^2=2(cm)
d=căn 2^2+1^2=căn 5(cm)
e=căn 6
f=căn 7
g=căn 8
h=căn 9
i=căn 10
j=căn 11
k=căn 12
l=căn 13
m=căn 14
Đúng 0
Bình luận (0)
Biết độ dài các cạnh của một tam giac tỉ lệ thuận với 3;5;7 tính các cạnh của tam giác nếu: Tổng độ dài cạnh lớn nhất và cạnh nhỏ nhất hơn cạnh còn lại 20 cm
Gọi độ dài của các cạnh tam giác đó lần lượt là x;y;z ( cm )
Theo đề bài ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\) và z - x = 20
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{z-x}{7-3}=\frac{20}{4}=5\)
\(\Rightarrow\frac{x}{3}=5\Rightarrow x=3.5=15\)
\(\frac{y}{5}=5\Rightarrow y=5.5=25\)
\(\frac{z}{7}=5\Rightarrow z=7.5=35\)
Vậy độ dài ba cạnh của tam giác lần lượt là 15 cm , 25 cm , 35 cm
Đúng 1
Bình luận (0)
theo bài ra ta có:a/3=b/5=c/7
và (a+c)-b=20
áp dụng....ta có;
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{a+c-b}{3+7-5}=\frac{20}{5}=4\)
từ a/3=4=>a=12
b/5=4=>b=20
c/7=4=>c=28
vậy.......
Đúng 0
Bình luận (0)
gọi độ dài 3 cạnh lần lượt là x;y;z (x lớn nhất và z nhỏ nhất )
ta có : z/3=y/5=x/7 và x-z=20cm
áp dụng ... ta có :
x/7=z/3=x-z/7-3=20/4=5
=>x/7=5=>x=35cm
=>y/5=5=>y=25cm
=>z/3=5=>z=15cm
Đúng 0
Bình luận (0)
Trên một mảnh đất hình vuông , người ta đào một cái ao cũng hình vuông nên diện tích đất còn lại là 8400 mét vuông . Tính diện tích cái ao . Biết cạnh mảnh đất hơn cạnh ao là 70 m
Bài 2 : tìm y
y x 75 + y x 96 + y = 7912
[ y : 46 - 12 * 23 ] x 24 = 3696
các bạn giải đầy đủ mình sẽ like cho nhé mình rat cần ngay bây giờ
Câu 1: Cho hình chữ nhật ABCD, Nếu cạnh AB tăng 20%, cạnh BC giảm 20% thì diện tích hình chữ nhật giảm 30m vuông. Tìm diện tích hình chữ nhật ABCD.Câu 2: Tìm các cặp số nguyên x, y thỏa mãn điều kiện 3/x +y/3 5/6.Câu 3: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a nhân với 5/12 và 10/21 ta đều được kết quả là các số tự nhiên.Câu 4: Cho hình chữ nhật ABCD, cạ AB tăng 36m, cạnh BC giảm 16%. Tìm độ dài cạnh AB sau khi tăng biết diện tích mới lớn hơn diện tích cũ là 5%.Câu 5: Lớp 6A có số học sinh...
Đọc tiếp
Câu 1: Cho hình chữ nhật ABCD, Nếu cạnh AB tăng 20%, cạnh BC giảm 20% thì diện tích hình chữ nhật giảm 30m vuông. Tìm diện tích hình chữ nhật ABCD.
Câu 2: Tìm các cặp số nguyên x, y thỏa mãn điều kiện 3/x +y/3 = 5/6.
Câu 3: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a nhân với 5/12 và 10/21 ta đều được kết quả là các số tự nhiên.
Câu 4: Cho hình chữ nhật ABCD, cạ AB tăng 36m, cạnh BC giảm 16%. Tìm độ dài cạnh AB sau khi tăng biết diện tích mới lớn hơn diện tích cũ là 5%.
Câu 5: Lớp 6A có số học sinh giỏi học kì 1 bằng 3/7 số còn lại. Cuối năm có them 4 học sinh đạt loại giỏi nên số học sinh giỏi bằng 2/3 số còn lại. Tìm số học sinh lớp 6A.
LÀM GIÚP MÌNH VỚI !
Câu 1: Cho hình chữ nhật ABCD, Nếu cạnh AB tăng 20%, cạnh BC giảm 20% thì diện tích hình chữ nhật giảm 30m vuông. Tìm diện tích hình chữ nhật ABCD.Câu 2: Tìm các cặp số nguyên x, y thỏa mãn điều kiện 3/x +y/3 5/6.Câu 3: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a nhân với 5/12 và 10/21 ta đều được kết quả là các số tự nhiên.Câu 4: Cho hình chữ nhật ABCD, cạ AB tăng 36m, cạnh BC giảm 16%. Tìm độ dài cạnh AB sau khi tăng biết diện tích mới lớn hơn diện tích cũ là 5%.Câu 5: Lớp 6A có số học sinh...
Đọc tiếp
Câu 1: Cho hình chữ nhật ABCD, Nếu cạnh AB tăng 20%, cạnh BC giảm 20% thì diện tích hình chữ nhật giảm 30m vuông. Tìm diện tích hình chữ nhật ABCD.
Câu 2: Tìm các cặp số nguyên x, y thỏa mãn điều kiện 3/x +y/3 = 5/6.
Câu 3: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a nhân với 5/12 và 10/21 ta đều được kết quả là các số tự nhiên.
Câu 4: Cho hình chữ nhật ABCD, cạ AB tăng 36m, cạnh BC giảm 16%. Tìm độ dài cạnh AB sau khi tăng biết diện tích mới lớn hơn diện tích cũ là 5%.
Câu 5: Lớp 6A có số học sinh giỏi học kì 1 bằng 3/7 số còn lại. Cuối năm có them 4 học sinh đạt loại giỏi nên số học sinh giỏi bằng 2/3 số còn lại. Tìm số học sinh lớp 6A.
Câu 1: Cho hình chữ nhật ABCD, Nếu cạnh AB tăng 20%, cạnh BC giảm 20% thì diện tích hình chữ nhật giảm 30m vuông. Tìm diện tích hình chữ nhật ABCD.Câu 2: Tìm các cặp số nguyên x, y thỏa mãn điều kiện 3/x +y/3 5/6.Câu 3: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a nhân với 5/12 và 10/21 ta đều được kết quả là các số tự nhiên.Câu 4: Cho hình chữ nhật ABCD, cạ AB tăng 36m, cạnh BC giảm 16%. Tìm độ dài cạnh AB sau khi tăng biết diện tích mới lớn hơn diện tích cũ là 5%.Câu 5: Lớp 6A có số học sinh...
Đọc tiếp
Câu 1: Cho hình chữ nhật ABCD, Nếu cạnh AB tăng 20%, cạnh BC giảm 20% thì diện tích hình chữ nhật giảm 30m vuông. Tìm diện tích hình chữ nhật ABCD.
Câu 2: Tìm các cặp số nguyên x, y thỏa mãn điều kiện 3/x +y/3 = 5/6.
Câu 3: Tìm số tự nhiên a nhỏ nhất khác 0 biết rằng a nhân với 5/12 và 10/21 ta đều được kết quả là các số tự nhiên.
Câu 4: Cho hình chữ nhật ABCD, cạ AB tăng 36m, cạnh BC giảm 16%. Tìm độ dài cạnh AB sau khi tăng biết diện tích mới lớn hơn diện tích cũ là 5%.
Câu 5: Lớp 6A có số học sinh giỏi học kì 1 bằng 3/7 số còn lại. Cuối năm có them 4 học sinh đạt loại giỏi nên số học sinh giỏi bằng 2/3 số còn lại. Tìm số học sinh lớp 6A.
Cho tam giác DEF vuông tại D . Tính các góc và cạnh còn lại , biết:
a. góc E = 60 độ , DE = 12 cm
b. DE = 15 cm , DF = 8 cm
a) Ta có: ΔDEF vuông tại D(gt)
nên \(\widehat{F}+\widehat{E}=90^0\)
hay \(\widehat{F}=30^0\)
Xét ΔDEF vuông tại D có
\(DF=DE\cdot\tan60^0\)
\(=12\sqrt{3}\left(cm\right)\)
Xét ΔDEF vuông tại D có
\(\sin\widehat{DFE}=\dfrac{DE}{FE}\)
\(\Leftrightarrow FE=12:\dfrac{1}{2}=24\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔDEF vuông tại D có
\(FE^2=DE^2+DF^2\)
\(\Leftrightarrow FE^2=8^2+15^2=289\)
hay FE=17(cm)
Xét ΔDEF vuông tại D có
\(\sin\widehat{DFE}=\dfrac{DE}{EF}=\dfrac{15}{17}\)
\(\Leftrightarrow\widehat{DFE}\simeq62^0\)
\(\Leftrightarrow\widehat{DEF}=28^0\)
Đúng 1
Bình luận (0)




















