Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:

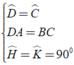
⇒ Δ ADH = Δ BCK

(trường hợp cạnh huyền – góc nhọn)

⇒ DH = CK (cặp cạnh tương ứng bằng nhau)

Vậy DH = CK. (đpcm)

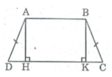
Xét hai tam giác vuông AHD và BKC:

∠ (AHD) =  ∠ (BKC) = 90 0

AD = BC (tính chất hình thang cân)

∠ C = ∠ D (gt)

Suy ra: ∆ AHD =  ∆ BKC (cạnh huyền, góc nhọn)

⇒ HD = KC

Xét tam giác AHD vuông tại H và tam giác BKC vuông tại K

Ta có: AD= BC (gt)

          Góc D = góc C

=> tam giác AHD= tam giác BKC (cạnh huyền- góc nhọn)

=> DH= CK ( 2 cạnh tương ứng)

xét tam giác AHD và tam giác BKC có:

            AD = BC (gt)

              góc ADH = góc BCK (gt)

                   góc AHD = góc AKC = 90⁰

=> tam giác ... = tam giác .... (ch-gn)

=> DH = CK (cạnh tương ứng)

t i c k nha!! 463745768658897697696789768568654

Có hình thang ABCD cân

⇒AD=BC ; ∠ADC=∠BCD

Có AH⊥DC

⇒∠AHD=∠AHC

Có BK⊥DC

⇒∠BKC=∠BKD

* Xét △AHD(∠AHD=90) và ΔBKC(∠BKC=90) có

AD=BC(c/m trên)

∠ADH=∠BCK

⇒△AHD=ΔBKC( cạnh huyền-góc nhọn)

⇒DH=KC(2 cạnh tương ứng)(đpcm)

Xét hình thang cân ABCD ( AB // CD )

\(\Rightarrow\hept{\begin{cases}\widehat{D}=\widehat{C}\\AD=BC\end{cases}\left(t/c\right)}\)

Xét \(\Delta ADH=\Delta BCK\)

\(\hept{\begin{cases}\widehat{AHD}=\widehat{BKC}\left(=90^o\right)\\AD=BC\left(cmt\right)\\\widehat{D}=\widehat{C}\left(cmt\right)\end{cases}}\)

\(\Rightarrow\Delta ADH=\Delta BCK\)  ( ch - gn )

\(\Rightarrow AH=BK\) ( 2 cạnh tương ứng )
 b) Vì \(\Delta ADH=\Delta BCK\left(cmt\right)\)

\(\Rightarrow DK=CK\) ( 2 cạnh tương ứng )

Chúc bạn học tốt !!!

Xét hai tam giác vuông AHD và BKC:

ˆAHD=ˆBKC=90 độ

AD=BC (tính chất hình thang cân)

ˆC=ˆD (gt)

Do đó: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)

=> đpcm

Xét tam giác bằng nhau là ra