
Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
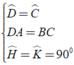
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)

Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
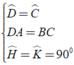
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)
cho hình thang cân ABCD(AB//CD, AB<CD) kẻ đường cao AH,BK của hình thang. chứng minh rằng DH=CK
Hình thang cân ABCD có AB //CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DH = CK
hình thang cân ABCD có AB // CD , AB < CD .kẻ các đường cao AH , BK. Chứng minh rằng DH = CK
cho hình thang cân ABCD (AB//CD) , AB<CD . Kẻ các đường cao AH , BK . Chứng minh rằng :
a) AH=BK
b) DH=CK
Bài 6. Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AH, BK của hình thang.
a) Chứng minh rằng DH = CK.
b) Cho biết AB = AH , AD =15 cm , DH =9 . Tính DC
Hình thang cân ABCD có AB // CD , AB < CD. Kẻ các đường cao AH , BK
a) Chứng minh DH = CK
b) Tính các góc của hình thang cân biết Góc C = 50 độ
Cho hình thang cân ABCD có AB // CD, AB < CD. Kẻ đường cao AH, BK.
a, Chứng minh rằng : DH = CK.
b, Biết AB = 6cm; BC = 15cm. Tính HD, KC
Cho hình thang cân ABCD (AB//CD) có AH và BK là 2 đường cao của hình thang
a) Chứng minh rằng: DH = CD - AB/2
b) Biết AB = 6cm; CD = 14 cm; AD = 5cm
Tính DH; AH và diện tích hình thang ABCD
Cho hình thang cân ABCD ( AB//CD) và AB < CD, kẻ đường cao AH, BK. C/m DH=CK. Cho AD =10 cm , DH =6 cm. Tính BK