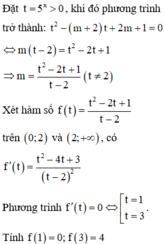Nghiệm nhỏ nhất của phương trình
x3-6x2-25x-18=0 là x bằng bao nhiêu?

Những câu hỏi liên quan
Nghiệm nhỏ nhất của phương trình x3-6x2-25x-18=0 là x=?
\(x^3-6x^2-25x-18=0\)
<=> \(x^3-9x^2+3x^2-27x+2x-18=0\)
<=> \(x^2\left(x-9\right)+3x\left(x-9\right)+2\left(x-9\right)=0\)
<=> \(\left(x-9\right)\left(x^2+3x+2\right)=0\)
<=> \(\left(x-9\right)\left(x+1\right)\left(x+2\right)=0\)
..................
làm nốt
Đúng 0
Bình luận (0)
nghiệm nhỏ nhất của phương trình : x3-6x2-25x-18 =0
Ta có:\(x^3-6x^2-25x-18=0\Leftrightarrow x^3+2x^2-8x^2-16x-9x-18=0\Leftrightarrow x^2\left(x+2\right)-8x\left(x+2\right)-9\left(x+2\right)=0\)\(\Leftrightarrow\left(x+2\right)\left(x^2+x-9x-9\right)=0\Leftrightarrow\left(x+2\right)\left(x+1\right)\left(x-9\right)=0\)
Vậy x=-2;-1;9 hay x min = -2
Đúng 0
Bình luận (0)
Nghiệm nhỏ nhất của phương trình x3 - 6x2 - 25x - 18 = 0
(ghi cach giai rõ ràng dùm mình)
Ta có:x^3-6x^2-25x-18=0 <=> x^3+2x^2-8x^2-16x-9x-18=0
<=> x^2 (x+2)-8x(x+2)-9(x+2)=0 <=> (x+2)(x2+x−9x−9)=0⇔(x+2)(x+1)(x−9)=0
Vậy x=-2;-1;9 hay x min = -2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho phương trình
y
x
3
-
6
x
2
+
9
x
-
2
và các phát biểu sau:(1) x 0 là nghiệm duy nhất của phương trình(2) Phương trình có nghiệm dương (3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1(4) Phương trình trên có tổng 2 nghiệm là:
-
log...
Đọc tiếp
Cho phương trình y = x 3 - 6 x 2 + 9 x - 2 và các phát biểu sau:
(1) x = 0 là nghiệm duy nhất của phương trình
(2) Phương trình có nghiệm dương
(3) Cả 2 nghiệm của phương trình đều nhỏ hơn 1
(4) Phương trình trên có tổng 2 nghiệm là: - log 5 3 7
Số phát biểu đúng là:
A. 1
B. 2
C. 3
D. 4
Cho (x; y; z) là nghiệm của hệ phương trình
36
x
2
y
−
60
x
2
+
25
y
0
36...
Đọc tiếp
Cho (x; y; z) là nghiệm của hệ phương trình 36 x 2 y − 60 x 2 + 25 y = 0 36 y 2 z − 60 y 2 + 25 z = 0 36 z 2 x − 60 z 2 + 25 x = 0 . Giá trị nhỏ nhất của A = x + y + z là:
A. A = 0
B. A = 5 2
C. A = 1
D. A = −2
36 x 2 y − 60 x 2 + 25 y = 0 36 y 2 z − 60 y 2 + 25 z = 0 36 z 2 x − 60 z 2 + 25 x = 0 ⇔ y = 60 x 2 36 x 2 + 25 z = 60 y 2 36 y 2 + 25 x = 60 z 2 36 z 2 + 25 ⇒ x , y , z ≥ 0
Nhận thấy x = y = z = 0 là một nghiệm của hệ phương trình
Xét x > 0; y > 0; z > 0 áp dụng bất đẳng thức Cosi cho hai số không âm ta có:
36 x 2 + 25 ≥ 2 36 x 2 .25 = 60 | x | ≥ 60 x ⇒ y ≤ x
Chứng minh tương tự, ta được z ≤ y ; x ≤ z ⇒ x ≤ z ≤ y ≤ x ⇒ x = y = z
Thay vào phương trình (1) ta được 36 x 3 – 60 x 2 + 25 x = 0 ⇔ x = 5 6
hay x = y = z = 5 6
Suy ra giá trị nhỏ nhất của A = x + y + z = 0 (khi x = y = z = 0)
Đáp án:A
Đúng 0
Bình luận (0)
Cho phương trình
25
x
-
m
+
2
5
x
+
2
m
+
1
0
, m là tham số thực. Có bao nhiêu giá trị nguyên của
m
∈
0
;
2018
để phương trình có nghiệm? A. 2015 B. 2016 C. 2018 D. 2017
Đọc tiếp
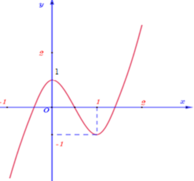
Cho phương trình 25 x - m + 2 5 x + 2 m + 1 = 0 , m là tham số thực. Có bao nhiêu giá trị nguyên của m ∈ 0 ; 2018 để phương trình có nghiệm?
A. 2015
B. 2016
C. 2018
D. 2017
Nghiệm dương nhỏ nhất của phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\) là bao nhiêu?
Xét phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\)
\(\begin{array}{l} \Leftrightarrow sin\left( {x + \frac{\pi }{6}} \right) = sin2x.\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{6} = 2x + k2\pi \\x + \frac{\pi }{6} = \pi - 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Với \(x = \frac{\pi }{6} + k2\pi \) có nghiệm dương bé nhất là \(x = \frac{\pi }{6}\) khi \(k = 0\).
Với \(x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\) có nghiệm dương bé nhất là \(x = \frac{{5\pi }}{{18}}\) khi \(k = 0\).
Vậy nghiệm dương bé nhất của phương trình đã cho là \(x = \frac{\pi }{6}\).
Đúng 0
Bình luận (0)
Cho hàm số
y
4
x
3
-
6
x
2
+
1
có đồ thị là đường cong trong hình dưới đây. Khi đó phương trình
4
4
x
3
-
6
x...
Đọc tiếp
Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
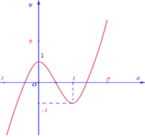
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
Cho hàm số
y
4
x
3
-
6
x
2
+
1
có đồ thị là đường cong trong hình dưới đây. Khi đó phương trình
4
4
x
3
-
6
x...
Đọc tiếp
Cho hàm số y = 4 x 3 - 6 x 2 + 1 có đồ thị là đường cong trong hình dưới đây.
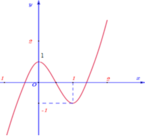
Khi đó phương trình 4 4 x 3 - 6 x 2 + 1 3 - 6 4 x 3 - 6 x 2 + 1 2 + 1 = 0 có bao nhiêu nghiệm thực.
A. 9
B. 6
C. 7
D. 3
Đáp án C
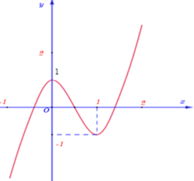

Vậy phương trình đã cho có 7 nghiệm thực.
Đúng 0
Bình luận (0)