trong mặt phẳng tọa độ Oxy , cho đường thẳng (Δ) : ax + by + c = 0 và điểm I(x0 ; y0) . Phép đối xứng tâm ĐI biến đường thẳng Δ thành đường thẳng Δ' . Viết phương trình của Δ'.

Những câu hỏi liên quan
trong mặt phẳng tọa độ Oxy , cho đường thẳng (d) : ax + by + c = 0 và điểm I(x0 ; y0) . Phép đối xứng tâm ĐI biến đường thẳng (d) thành đường thẳng (d') . Viết phương trình của (d')
trong mặt phẳng tọa độ Oxy cho đồ thị hàm số y=ax là đường thẳng OM với M(-3;2).Điểm N(x0;y0)thuộc đồ thị hàm số trên.Tính x0-3/y0+2
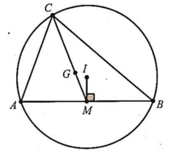
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I(2;1), tọng tâm
G
7
3
;
4
3
, phương trình đường thẳng AB: x-y+10. Giả sử điểm
C
(
x
0
;
y
0
)
, tính
2
x
0...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I(2;1), tọng tâm G 7 3 ; 4 3 , phương trình đường thẳng AB: x-y+1=0. Giả sử điểm C ( x 0 ; y 0 ) , tính 2 x 0 + y 0
A. 18.
B. 10
C. 9.
D. 12
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC cân tại B với A(1;-1), C(3;5). Điểm B nằm trên đường thẳng d: 2x - y = 0. Phương trình các đường thẳng AB, BC lần lượt là ax + by - 24 = 0, cx + dy + 8 = 0. Tính giá trị biểu thức a.b.c.d.
Giả sử I(xI;yI) là trung điểm của AC
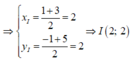
Vì tam giác ABC cân tại B nên BI ⊥ AC. Phương trình đường thẳng BI đi qua I(2;2) nhận 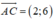 làm VTPT là:
làm VTPT là:
2.(x - 2) + 6.(y - 2) = 0 ⇔ 2x - 4 + 6y - 12 = 0 ⇔ 2x + 6y - 16 = 0 ⇔ x + 3y - 8 = 0
Tọa độ giao điểm B của BI và d là nghiệm của hệ phương trình:
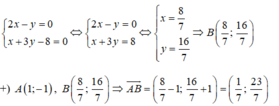
Phương trình đường thẳng AB đi qua A(1;-1) nhận 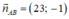 làm VTPT là:
làm VTPT là:
23.(x - 1) - 1.(y + 1) = 0 ⇔ 23x - 23 - y - 1 = 0 ⇔ 23x - y - 24 = 0
⇒ a = 23; b = -1
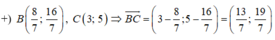
Phương trình đường thẳng BC đi qua C(3;5) nhận 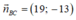 làm VTPT là:
làm VTPT là:
19.(x - 3) + (-13).(y - 5) = 0 ⇔ 19x - 57 - 13y + 65 = 0 ⇔ 19x - 13y + 8 = 0
⇒ c = 19; d = -13
⇒ a.b.c.d = 23.(-1).19.(-13) = 5681
Vậy a.b.c.d = 5681.
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho đường tròn
(
C
)
:
x
-
4
2
+
y
-
3
2
5
và đường thẳng d: x+2y-50. Tọa độ tiếp điểm M của đường thẳng d và đường tròn (C) là A. M(3;1) B. M(6;4) C. M(5;0) D. M(1;2)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn ( C ) : x - 4 2 + y - 3 2 = 5 và đường thẳng d: x+2y-5=0. Tọa độ tiếp điểm M của đường thẳng d và đường tròn (C) là
A. M(3;1)
B. M(6;4)
C. M(5;0)
D. M(1;2)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn
C
:
x
+
1
2
+
y
-
2
2
9
và điểm
I
-
3
;
3
. Đường thẳng...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C : x + 1 2 + y - 2 2 = 9 và điểm I - 3 ; 3 . Đường thẳng ∆ : a x + b + c = 0 đi qua điểm I và cắt đường tròn (C) tại hai điểm A và B. Tiếp tuyến của A và B cắt nhau tại M. Biết điểm M thuộc đường thẳng x + 3 y - 4 = 0 . Tính P = 2 a + 3 b c
A. P = 1 3
B. P = - 11 4
C. P = 2 3
D. P = 1 4
Đáp án A.
Đường tròn (C) có tâm K(-1;2) và bán kính R = 3


Vậy phương trình đường thẳng D là
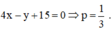
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy , cho đường thẳng (\(\Delta\)) : ax + by + c = 0 và điểm I(x0 ; y0) . Phép đối xứng tâm ĐI biến đường thẳng \(\Delta\) thành đường thẳng \(\Delta\)' . Viết phương trình của \(\Delta\)'
Cho hai đường thẳng (D): y = - x - 4 và (D1) : y = 3x + 2
a) Vẽ đồ thị (D) và (D1) trên cùng 1 mặt phẳng tọa độ Oxy
b) Xác định tọa độ giao điểm A của hai đường thẳng (D) và (D1) bằng phép toán
c) Viết phương trình đường thẳng (D2): y = ax + b (a ≠ 0) song song với đường thẳng (D) và đi qua điểm B(-2;5)
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
Đúng 1
Bình luận (0)
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
Đúng 0
Bình luận (0)
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 0 a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng 4sqrt{5}.Tìm tọa độ các giao điểm của d và (C)b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng 5sqrt{3}
Đọc tiếp
Trong mặt phẳng tọa độ Oxy , cho điểm I (-1;2) và đường thẳng d: x+3y+5 = 0
a) Viết phương trình đường tròn (C) có tâm I và đường kính bằng \(4\sqrt{5}\).Tìm tọa độ các giao điểm của d và (C)
b) Viết phương trình đường thằng Δ vuông góc với d và căt (C) tại hai điểm phân biệt A,B sao cho tam giác IAB tù và có diện tích bằng \(5\sqrt{3}\)
a, Bán kính: \(R=2\sqrt{5}\)
Phương trình đường tròn: \(\left(x+1\right)^2+\left(y-2\right)^2=20\)
Giao điểm của d và (C) có tọa độ là nghiệm hệ:
\(\left\{{}\begin{matrix}\left(x+1\right)^2+\left(y-2\right)^2=20\\x+3y+5=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(3y+4\right)^2+\left(y-2\right)^2=20\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10y^2+20y=0\\x=-3y-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}y=0\\x=-5\end{matrix}\right.\\\left\{{}\begin{matrix}y=-2\\x=1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}M=\left(0;-5\right)\\N=\left(-2;1\right)\end{matrix}\right.\) là các giao điểm
b, Gọi H là trung điểm AB.
Đường thẳng \(\Delta\) vuông góc với d nên có phương trình dạng: \(3x-y+m=0\left(m\in R\right)\)
Ta có: \(S_{IAB}=\dfrac{1}{2}.R^2.sinAIB=10.sinAIB=5\sqrt{3}\)
\(\Rightarrow sinAIB=\dfrac{\sqrt{3}}{2}\)
Mà tam giác ABC tù nên \(\widehat{AIB}=120^o\)
\(\Rightarrow\widehat{HBI}=30^o\)
Khi đó:
\(IH=d\left(I;\Delta\right)\)
\(\Leftrightarrow R.sinHBI=\dfrac{\left|-3-2+m\right|}{\sqrt{10}}\)
\(\Leftrightarrow2\sqrt{5}.sin30^o=\dfrac{\left|m-5\right|}{\sqrt{10}}\)
\(\Leftrightarrow m=5\pm5\sqrt{2}\)
\(\Rightarrow\left[{}\begin{matrix}\Delta:3x-y+5+5\sqrt{2}=0\\\Delta:3x-y+5-5\sqrt{2}=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy, cho điểm M (-1;2) và đường thẳng d: 4x-3y+5=0. Tìm tọa độ điểm N thuộc đường thẳng d và cách điểm N một khoảng bằng 1
d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)
Đúng 0
Bình luận (0)