hình H1 gồm ba đường tròn (O1 ; r1) , (O2 ; r2) , (O3 ; r3) đôi một tiếp xúc ngoài với nhau . Hình H2 gồm ba đường tròn (I1 ; r1) , (I2 ; r2) , (I3 ; r3) đôi một tiếp xúc ngoài với nhau . Chứng tỏ rằng 2 hình H1 và H2 bằng nhau .

Những câu hỏi liên quan
Cho hình vẽ bên có hai đường tròn (O; 3cm) và (
O
1
; 3cm). Điểm
O
1
nằm trên đường tròn tâm O.a) Vẽ đường tròn tâm A, bán kính 3cm.b) Vì sao đường tròn (A; 3cm) đi qua O và
O
1
?
Đọc tiếp
Cho hình vẽ bên có hai đường tròn (O; 3cm) và ( O 1 ; 3cm). Điểm O 1 nằm trên đường tròn tâm O.
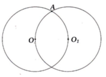
a) Vẽ đường tròn tâm A, bán kính 3cm.
b) Vì sao đường tròn (A; 3cm) đi qua O và O 1 ?
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O1 vì OA = O 1 A = 3 cm.
Đúng 0
Bình luận (0)
Cho hình vẽ bên có hai đường tròn (O; 3cm) và (
O
1
; 3cm). Điểm
O
1
nằm trên đường tròn tâm O.a) Vẽ đường tròn tâm A, bán kính 3cm.b) Vì sao đường tròn (A; 3cm) đi qua O và
O
1
?
Đọc tiếp
Cho hình vẽ bên có hai đường tròn (O; 3cm) và ( O 1 ; 3cm). Điểm O 1 nằm trên đường tròn tâm O.
a) Vẽ đường tròn tâm A, bán kính 3cm.
b) Vì sao đường tròn (A; 3cm) đi qua O và O 1 ?
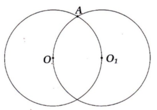
a) HS tự vẽ hình.
b) Đường tròn (A; 3cm) đi qua O và O 1 vì O A = O 1 A = 3 c m .
Đúng 0
Bình luận (0)
Một khối trụ tròn có thể tích là V, các đường tròn đáy có tâm là
O
1
,
O
2
(hình vẽ). Xét hình nón
N
1
đỉnh
O
1
, đáy là đường tròn đáy tâm
O
2
của hình trụ, hình nón
N
2
đỉnh
O
2
, đáy là đ...
Đọc tiếp
Một khối trụ tròn có thể tích là V, các đường tròn đáy có tâm là O 1 , O 2 (hình vẽ). Xét hình nón N 1 đỉnh O 1 , đáy là đường tròn đáy tâm O 2 của hình trụ, hình nón N 2 đỉnh O 2 , đáy là đường tròn đáy tâm O 1 của hình trụ. Gọi V O là phần thể tích chung của N 1 , N 2 . Tính k = V O V
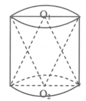
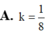
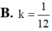
![]()
![]()
Cho H,K là giao điểm của hai đường tròn tâm O1 và O2.Đường thẳng O1H cắt đường tròn O1 tại A và đường tròn tâm O2 tại B.Đường thẳng O2H cắt đường tròn tâm O1 tại C và đường tròn tâm O2 tại D.Chứng minh:
a, Ba đường thẳng AC,BD,HK đồng quy tại một điểm
b, BH.BA=CH.CD
Cho hai đường tròn O, O1 tiếp xúc ngoài nhau tại A. Trên đường tròn O lấy hai điểm phân biệt B, C khác A. Các đường thẳng BA, CA cắt đường tròn O1 lần lượt tại P,Q. cm PQ song song BC
Bạn Nhẫn đi làm 1 cây đàn mặt đàn như hình vẽ gồm 1 hình thang ghép với 2 nửa hình tròn tâm O1 có d=30cm,tâm O2 có d=20cm khoảng cách giữa O1 và O2 là 35cm.Mặt đàn khoét 1 hình tròn tâm O3 d=8cm.Tính S mặt đàn của bạn Nhẫn
BÀI 10.Hãy vẽ hai đường trònC1(O1,R1)vàC1(O2,R2)sao cho hai đường tròn nàycắt nhau tại hai điểm phân biệtA,Btrong hai trường hợp:
1.O1,O2khác phía đường thẳngAB;
2.O1,O2cùng phía đường thẳngAB. mong mn giups mik và vẽ hình với ạ
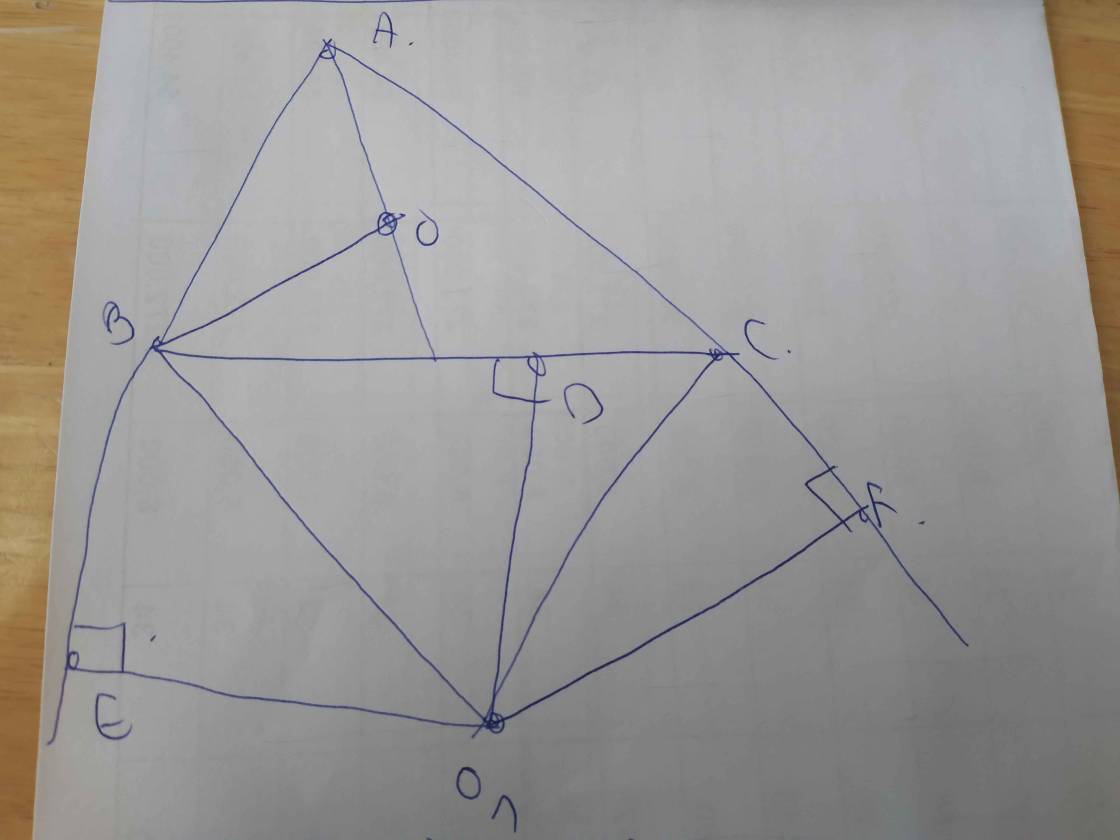
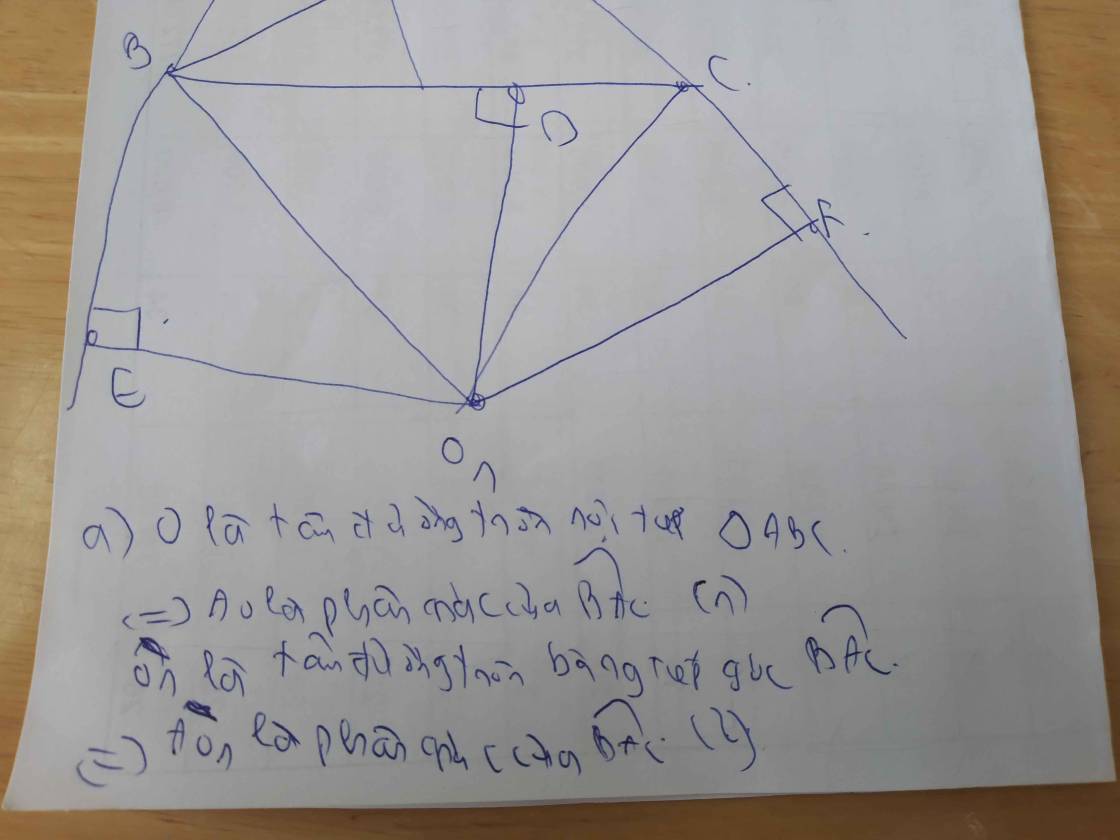
Cho tam giác ABC có AB = 5cm, AC = 7cm, BC = 6cm ngoại tiếp đường tròn (O). Đường tròn (O1) bằng tiếp góc A tiếp xúc với cạnh BC ở D, tiếp xúc với phần kéo dài của các cạnh AB, AC lần lượt ở E và F.
a) Chứng minh ba điểm A, O, O1, thẳng hàng
b) Tính độ dài các đoạn AE, AF. BE, CF
Cho (O) cát (O1) tại A và B. Tiếp tuyến tại A của (O) và (O1) cắt (O1) và (O) tại E, F. Gọi I là tâm đường tròn ngoại tiếp \(\Delta\)EAF.
a) CM tứ giác OaO1I là hình bình hành. OO1 // BI
b) CM tứ giác OBIO1 nội tiếp
c) C thuộc tia đối BA mà BA = CB. CMR tứ giác AECF nội tiếp (O)
o ba đường tròn (o),(o1),(o2) có bán kình r,r1,r2 tiếp xúc ngoài đôi một. tìm độ dài dây ab mà tiếp tuyến chung ngoài cua (0) và (o1) cắt (02) theo r,r1,r2