Bài 4: 

2: Xét ΔBAK vuông tại A có AD là đường cao ứng với cạnh huyền BK

nên \(BD\cdot BK=BA^2\left(1\right)\)

Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC

nên \(BH\cdot BC=BA^2\left(2\right)\)

Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

Bài nào nhỉ

Bài 5: 

\(\cos\alpha=\sqrt{1-\dfrac{1}{25}}=\dfrac{2\sqrt{6}}{5}\)

\(\tan\alpha=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{\sqrt{6}}{12}\)

\(\cot\alpha=2\sqrt{6}\)

Bài 5: 

\(\cos\alpha=\sqrt{1-\dfrac{1}{25}}=\dfrac{2\sqrt{6}}{5}\)

\(\tan\alpha=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)

\(\cot\alpha=1:\dfrac{\sqrt{6}}{24}=4\sqrt{6}\)

\(5,\\ K=\sqrt{5x-9+6\sqrt{5x-9}+9}+\sqrt{5x-9-6\sqrt{5x-9}+9}\\ K=\sqrt{\left(\sqrt{5x-9}+3\right)^2}+\sqrt{\left(\sqrt{5x-9}-3\right)^2}\\ K=\sqrt{5x-9}+3+\sqrt{5x-9}-3=2\sqrt{5x-9}\ge0,\forall x\\ K_{min}=0\Leftrightarrow\sqrt{5x-9}=0\Leftrightarrow x=\dfrac{9}{5}\)

\(3,\\ 1,A=\dfrac{1,44+7}{\sqrt{1,44}}=\dfrac{7,44}{1,2}=\dfrac{31}{5}\\ 2,B=\dfrac{x-3\sqrt{x}+\left(2\sqrt{x}-1\right)\left(\sqrt{x}+3\right)-2x+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ B=\dfrac{x-3\sqrt{x}+2x+5\sqrt{x}-3-2x+\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)

\(3,S=\dfrac{1}{B}+A=\dfrac{\sqrt{x}+3}{\sqrt{x}}+\dfrac{x+7}{\sqrt{x}}=\dfrac{x+\sqrt{x}+10}{\sqrt{x}}\\ S=\sqrt{x}+1+\dfrac{10}{\sqrt{x}}\ge2\sqrt{\sqrt{x}\cdot\dfrac{10}{\sqrt{x}}}+1=2\sqrt{10}+1\left(BĐT.cosi\right)\)

Dấu \("="\Leftrightarrow x=10\)

\(1,HC=BC-HB=6\left(cm\right)\) 

Áp dụng HTL:

\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=16\\AC^2=CH\cdot BC=48\\AH^2=BH\cdot HC=12\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=4\left(cm\right)\\AC=4\sqrt{3}\left(cm\right)\\AH=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)

\(2,\widehat{ADB}=\widehat{AHB}\left(=90^0\right)\) nên \(ADHB\) nội tiếp

\(\Rightarrow\widehat{HDB}=\widehat{HAB}\left(cùng.chắn.HB\right)\)

Mà \(\widehat{HAB}=\widehat{ACB}\left(cùng.phụ.\widehat{HAC}\right)\)

\(\Rightarrow\widehat{HDB}=\widehat{ACB}\)

\(\left\{{}\begin{matrix}\widehat{HDB}=\widehat{ACB}\left(cm.trên\right)\\\widehat{KBC}.chung\end{matrix}\right.\Rightarrow\Delta BHD\sim\Delta BKC\left(g.g\right)\\ \Rightarrow\dfrac{BD}{BC}=\dfrac{BH}{BK}\Rightarrow BD\cdot BK=BH\cdot BC\)

\(c,\) Áp dụng công thức tính diện tích hình tam giác bằng 

Bài 4:

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có

\(\widehat{EAB}\) chung

Do đó: ΔAEB đồng dạng với ΔAFC

=>\(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)

=>\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

Xét ΔAEF và ΔABC có

\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)

\(\widehat{EAF}\) chung

Do đó: ΔAEF đồng dạng với ΔABC

=>\(\widehat{AEF}=\widehat{ABC}\)

b: Xét ΔBDH vuông tại D và ΔBEC vuông tại E có

\(\widehat{DBH}\) chung

Do đó: ΔBDH đồng dạng với ΔBEC

=>\(\dfrac{BD}{BE}=\dfrac{BH}{BC}\)

=>\(BD\cdot BC=BH\cdot BE\)

Xét ΔCDH vuông tại D và ΔCFB vuông tại F có

\(\widehat{DCH}\) chung

Do đó: ΔCDH đồng dạng với ΔCFB

=>\(\dfrac{CD}{CF}=\dfrac{CH}{CB}\)

=>\(CF\cdot CH=CD\cdot CB\)

\(BH\cdot BE+CF\cdot CH\)

\(=BD\cdot BC+CD\cdot BC\)

\(=BC\cdot\left(BD+CD\right)=BC^2\)

c: Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=180^0\)

=>BFHD là tứ giác nội tiếp

=>\(\widehat{FBH}=\widehat{FDH}\)

=>\(\widehat{FDH}=\widehat{ABE}\)

Xét tứ giác CEHD có

\(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)

=>CEHD là tứ giác nội tiếp

=>\(\widehat{HDE}=\widehat{HCE}\)

=>\(\widehat{HDE}=\widehat{ACF}\)

\(\widehat{FDH}=\widehat{ABE}\)

\(\widehat{HDE}=\widehat{ACF}\)

\(\widehat{ABE}=\widehat{ACF}\left(=90^0-\widehat{BAC}\right)\)

Do đó: \(\widehat{FDH}=\widehat{EDH}\)

=>DH là phân giác của góc FDE

Xét tứ giác AFHE có

\(\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0\)

=>AFHE là tứ giác nội tiếp

=>\(\widehat{HFE}=\widehat{HAE}=\widehat{DAC}\)

BFHD là tứ giác nội tiếp

=>\(\widehat{HFD}=\widehat{HBD}=\widehat{EBC}\)

\(\widehat{HFE}=\widehat{DAC}\)

\(\widehat{HFD}=\widehat{EBC}\)

\(\widehat{DAC}=\widehat{EBC}\left(=90^0-\widehat{ACB}\right)\)

Do đó: \(\widehat{HFE}=\widehat{HFD}\)

=>FH là phân giác của góc EFD

Xét ΔEFD có

FH,DH là các đường phân giác

FH cắt DH tại H

Do đó: H là tâm đường tròn nội tiếp ΔEDF

Câu c bài 3 ạ

\(B=\dfrac{x+2\sqrt{x}+3\sqrt{x}-6-9\sqrt{x}+10}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ B=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\\ c,P=B:A=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}-2}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}\\ P=\dfrac{\sqrt{x}+2-5}{\sqrt{x}+2}=1-\dfrac{5}{\sqrt{x}+2}\)

Ta có \(\sqrt{x}\ge0\Leftrightarrow\sqrt{x}+2\ge2\Leftrightarrow\dfrac{5}{\sqrt{x}+2}\le\dfrac{5}{2}\)

\(\Leftrightarrow P=1-\dfrac{5}{\sqrt{x}+2}\ge1-\dfrac{5}{2}=-\dfrac{3}{2}\\ P_{min}=-\dfrac{3}{2}\Leftrightarrow x=0\)

\(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}+\dfrac{3}{\sqrt{x}+2}+\dfrac{9\sqrt{x}-10}{4-x}\)

\(=\dfrac{x+2\sqrt{x}+3\sqrt{x}-6-9\sqrt{x}+10}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{x-4\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)

\(P=\dfrac{B}{A}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}:\dfrac{\sqrt{x}-2}{\sqrt{x}-3}=\dfrac{\sqrt{x}-2}{\sqrt{x}+2}.\dfrac{\sqrt{x}-3}{\sqrt{x}-2}=\dfrac{\sqrt{x}-3}{\sqrt{x}+2}=1-\dfrac{5}{\sqrt{x}+2}\)

Do \(\sqrt{x}+2\ge2\Rightarrow\dfrac{5}{\sqrt{x}+2}\le\dfrac{5}{2}\Rightarrow-\dfrac{5}{\sqrt{x}+2}\ge-\dfrac{5}{2}\)

\(\Rightarrow P=1-\dfrac{5}{\sqrt{x}+2}\ge1-\dfrac{5}{2}=-\dfrac{3}{2}\)

\(minP=-\dfrac{3}{2}\Leftrightarrow x=0\)

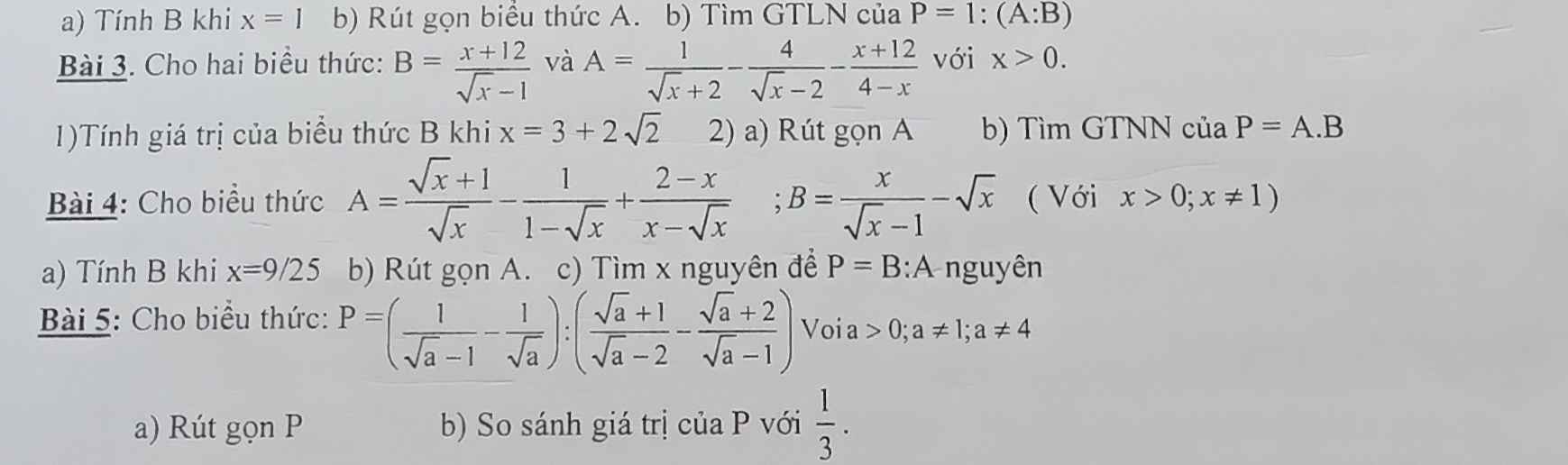
3:

1: Thay x=3+2căn 2 vào B, ta được:

\(B=\dfrac{3+2\sqrt{2}+12}{\sqrt{2}+1-1}=\dfrac{15+2\sqrt{2}}{\sqrt{2}}=\dfrac{15\sqrt{2}+4}{2}\)

2:

\(A=\dfrac{\sqrt{x}-2-4\sqrt{x}-8+x+12}{x-4}=\dfrac{x-3\sqrt{x}+2}{x-4}\)

\(=\dfrac{\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-1\right)}{x-4}=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)

\(P=A\cdot B=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\cdot\dfrac{x+2}{\sqrt{x}-1}=\dfrac{x+2}{\sqrt{x}+2}\)

\(=\dfrac{x-4+6}{\sqrt{x}+2}\)

\(=\sqrt{x}-2+\dfrac{6}{\sqrt{x}+2}\)

\(=\sqrt{x}+2+\dfrac{6}{\sqrt{x}+2}-4\)

=>\(P>=2\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{6}{\sqrt{x}+2}}-4=2\sqrt{6}=-4\)

Dấu = xảy ra khi (căn x+2)^2=6

=>căn x+2=căn 6

=>căn x=căn 6-2

=>x=10-4*căn 6