Tìm các tiệm cận : \(y=\sqrt{x^2+2x-5}\)

Những câu hỏi liên quan
Tìm các đường tiệm cận
\(y=\dfrac{\sqrt{-3x^2+2x+1}}{x}\)
Căn thức xác định khi \(-\dfrac{1}{3}\le x\le1\)
Do miền xác định này ko chứa vô cực nên hàm không có tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{-3x^2+2x+1}}{x}=\dfrac{1}{0}=\infty\Rightarrow x=0\) là tiệm cận đứng
Đúng 0
Bình luận (0)
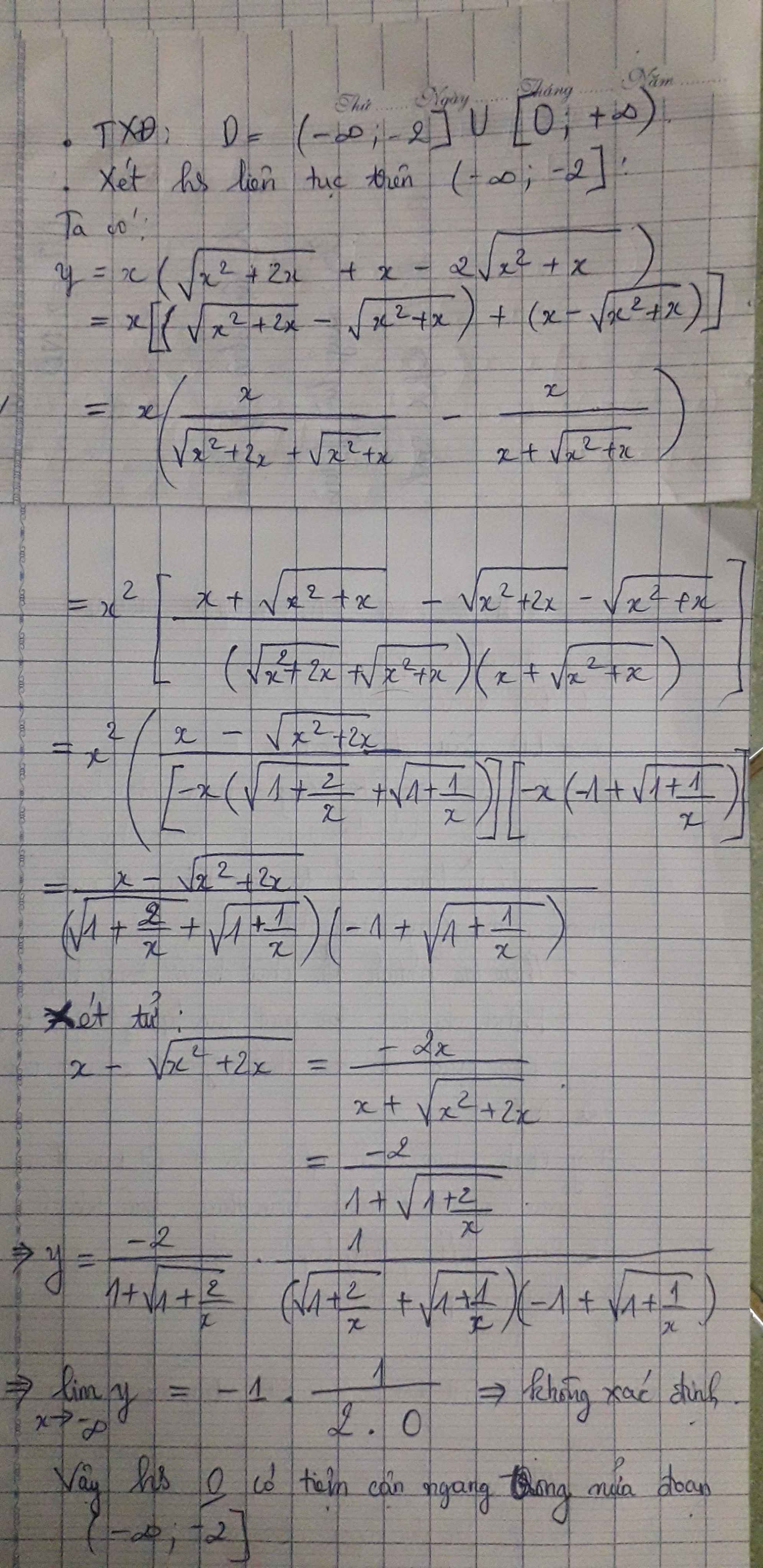
45. Tìm tất cả các đường tiệm cận ngang của đồ thi hs y = \(x.\left(\sqrt{x^2+2x}+x-2.\sqrt{x^2+x}\right)\)
45. Tìm tất cả các đường tiệm cận ngang của đồ thị hàm số y = \(x.\left(\sqrt{x^2+2x}+x-2\sqrt{x^2+x}\right)\)
Mọi người ơi cho mình hỏi bài này với ạ
1.Số đường tiệm cận của hàm số y=\(\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}\) là
2.Tìm tất cả các tiệm cận đứng của đồ thị hàm số y=\(\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}\)
Mình cảm ơn mọi người nhiều lắm !!!!!
1.
Điều kiện xác định của căn thức: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{1-1}{1}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{-1-1}{-1}=2\Rightarrow y=2\) là 1 TCN
\(\lim\limits_{x\rightarrow-5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}+5}{0}=+\infty\Rightarrow x=-5\) là 1 TCĐ
\(\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}-5}{0}=+\infty\Rightarrow x=5\) là 1 TCĐ
Hàm có 4 tiệm cận
Đúng 0
Bình luận (0)
2.
Căn thức của hàm luôn xác định
Ta có:
\(\lim\limits_{x\rightarrow2}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\lim\limits_{x\rightarrow2}\dfrac{\left(2x-1\right)^2-\left(x^2+x+3\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3x+1\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{3x+1}{\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}=\dfrac{-7}{6}\) hữu hạn
\(\Rightarrow x=2\) ko phải TCĐ
\(\lim\limits_{x\rightarrow3}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\dfrac{5-\sqrt{15}}{0}=+\infty\)
\(\Rightarrow x=3\) là tiệm cận đứng duy nhất
Đúng 0
Bình luận (0)
xác định đường tiệm cận ngang của đồ thị hàm số sau
a) \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
b) \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
a: \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{9+\dfrac{1}{x}}+1}{2+\dfrac{5}{x}}=\dfrac{\sqrt{9}+1}{2}=\dfrac{3+1}{2}=2\)
=>Đường thẳng y=2 là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{9+\dfrac{1}{x}}+1}{2+\dfrac{5}{x}}=\dfrac{-3+1}{2}=\dfrac{-2}{2}=-1\)
=>Đường thẳng y=-1 là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{9x^2+x}+x}{2x+5}\)
b: \(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{2+\dfrac{1}{x^2}}-1}{1+\dfrac{2}{x}}=\dfrac{\sqrt{2}-1}{1}=\sqrt{2}-1\)
=>Đường thẳng \(y=\sqrt{2}-1\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(\lim\limits_{x\rightarrow-\infty}y=\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{-\sqrt{2+\dfrac{1}{x^2}}-1}{1+\dfrac{2}{x}}=\dfrac{-\sqrt{2}-1}{1}=-\sqrt{2}-1\)
=>Đường thẳng \(y=-\sqrt{2}-1\) là một tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\sqrt{2x^2+1}-x}{x+2}\)
Đúng 1
Bình luận (0)
Nêu cách tìm ra tiệm cận ngang và tiệm cận dứng của đồ thị hàm số. Áp dụng để tìm các tiệm cận của đồ thị hàm số: Áp dụng để tìm các tiệm cận của đồ thị hàm số y = 2 x + 3 2 - x
- Cách tìm tiệm cận ngang:
+ Tính các giới hạn 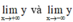
+ Nếu 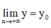 hoặc
hoặc 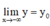 thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
- Cách tìm tiệm cận đứng:
Đường thẳng x = x o là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
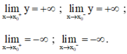
Đúng 0
Bình luận (0)
tìm m thỏa mãn yêu cầu bài toána) đồ thị hàm số ydfrac{mx-1}{2x+m} có đường tiệm cận đứng đi qua điểm A (-1;sqrt{2})b) đường thẳng x 1 là tiệm cận đứng của đồ thị hàm số ydfrac{x-2}{2x-m}c) biết đồ thị hàm số ydfrac{left(m+1right)x+2}{x-n+1} nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+nd) đồ thị hàm số ydfrac{x-1}{x^2+2left(m-1right)x+m^2-2} có 2 đường tiệm cận đứng
Đọc tiếp
tìm m thỏa mãn yêu cầu bài toán
a) đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\) có đường tiệm cận đứng đi qua điểm A (-1;\(\sqrt{2}\))
b) đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
c) biết đồ thị hàm số \(y=\dfrac{\left(m+1\right)x+2}{x-n+1}\) nhận trục hoành và trục tung làm 2 đường tiệm cận. Tính m+n
d) đồ thị hàm số \(y=\dfrac{x-1}{x^2+2\left(m-1\right)x+m^2-2}\) có 2 đường tiệm cận đứng
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow+\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
Vậy: x=m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\)
Để x=m/2 đi qua \(A\left(-1;\sqrt{2}\right)\) thì \(\dfrac{m}{2}=-1\)
=>\(m=-1\cdot2=-2\)
b: \(\lim\limits_{x\rightarrow-\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow-\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow+\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
=>x=1/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
=>Không có giá trị nào của m để đường thẳng x=1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
Đúng 0
Bình luận (0)
Nêu cách tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số. Áp dụng để tìm các đường tiệm cận của hàm số :
\(y=\dfrac{2x+3}{2-x}\)
tìm tiệm cận
\(y=\sqrt{x+\sqrt{x^2+x-1}}\)
Hàm không có tiệm cận đứng
Hàm không xác định khi \(x\rightarrow-\infty\)
\(\lim\limits_{x\rightarrow+\infty}\sqrt{x+\sqrt{x^2+x-1}}=+\infty\) ko hữu hạn
\(\Rightarrow\)Đồ thị hàm số không có tiệm cận
Đúng 0
Bình luận (0)