Cho điểm M(2,1)và đường thẳng d 3x+4y+10=0.Tìm ảnh của điểm M đối xứng qua đường thẳng d.

Những câu hỏi liên quan
Cho điểm M(5;2) và đường thẳng (d): 3x – y + 2 = 0. Tìm ảnh của M qua phép đối xứng qua đường thẳng (d)
A. (–5;4)
B. (5;4)
C. (4;5)
D. (–4;5)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 0 và đường tròn (C) có phương trình
x
2
+
y
2
−
2
x
+
4
y
–
4
0
. Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình 3x + 2y – 6 = 0 và đường tròn (C) có phương trình x 2 + y 2 − 2 x + 4 y – 4 = 0 . Tìm ảnh của M, d, và (C) qua phép đối xứng qua trục Ox
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
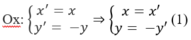
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
Đúng 0
Bình luận (0)
Cho đường thẳng d: 3x+ 4y – 10 = 0, điểm M(1; 2). Tìm toạ độ điểm H hình chiếu của M trên d và điểm M' đối xứng với M qua d.
Pt đường thẳng d' qua M và vuông góc d:
\(4\left(x-1\right)-3\left(y-2\right)=0\Leftrightarrow4x-3y+2=0\)
H là giao điểm d và d' nên tọa độ thỏa: \(\left\{{}\begin{matrix}3x+4y-10=0\\4x-3y+2=0\end{matrix}\right.\) \(\Rightarrow H\left(\frac{22}{25};\frac{46}{25}\right)\)
M' đối xứng M qua d \(\Leftrightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=\frac{19}{25}\\y_{M'}=2y_H-y_M=\frac{42}{25}\end{matrix}\right.\) \(\Rightarrow M'\left(\frac{19}{25};\frac{42}{25}\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho điểm M(3; -5), đường thẳng d có phương trình \(3x+2y-6=0\) và đường tròn (C) có phương trình \(x^2+y^2-2x+4y-4=0\). Tìm ảnh của M, d và (C) qua phép đối xứng qua trục Ox ?
4. Trong mặt phẳng Oxy, cho đường thẳng d: x − 3y + 1 = 0 và điểm I(−3; 1).
(a) Tìm ảnh của điểm M(1; −2) qua phép đối xứng tâm I.
(b) Tìm ảnh của đường thẳng ∆: 2x + y − 1 = 0 qua phép đối xứng tâm I.
(c) Tìm ảnh của đường tròn (C): (x − 2)2 + (y + 3)2 = 9 qua phép đối xứng
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 0 và đường tròn (C) có phương trình:
x
2
+
y
2
+
2
x
−
6
y
+
6
0
.Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đườn...
Đọc tiếp
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 = 0 và đường tròn (C) có phương trình: x 2 + y 2 + 2 x − 6 y + 6 = 0 .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .
Đúng 0
Bình luận (0)
1. Cho M(3;-1) và đường thẳng d: 3x-4y+120. Tìm N đối xứng với M qua d.2. Cho M(8;2) và đường thẳng d: 2x-3y+30. Tìm N đối xứng với M qua d.3. Cho đường thẳng d: x+y-50 và I(2;0). Tìm điểm M thuộc d sao cho MI3.4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-70 và d2: 5x+3y-290.a.Tìm điểm A và viết pt cạnh BC.b. Viết pt cạnh AC.CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
Đọc tiếp
1. Cho M(3;-1) và đường thẳng d: 3x-4y+12=0. Tìm N đối xứng với M qua d.
2. Cho M(8;2) và đường thẳng d: 2x-3y+3=0. Tìm N đối xứng với M qua d.
3. Cho đường thẳng d: x+y-5=0 và I(2;0). Tìm điểm M thuộc d sao cho MI=3.
4. Cho tam giác ABC có M(2;-1) là trung điểm AB. Đường trung tuyến và đường cao qua A lần lượt là: d1: x+y-7=0 và d2: 5x+3y-29=0.
a.Tìm điểm A và viết pt cạnh BC.
b. Viết pt cạnh AC.
CÁC BẠN GIẢI GIÚP MÌNH VỚI NHÉ. CẢM ƠN
trl ; bạn kia đúng r
-
_
----------------
Trong mặt phẳng Oxy cho điểm M(3;5) , đường thẳng d:3x+2y-4=0 và đường tròn c:x^2+y^2-2x+4y-4=0
a. Tìm ảnh của điểm M và đường thẳng d qua phép tịnh tiến theo vectơ = (2;1)
b. Tìm ảnh của đường tròn (C) qua phép quay tâm O góc quay 90 độ (O là gốc tọa độ).
Trong mặt phẳng tọa độ Oxy cho điểm A(4; – 1), đường thẳng (d) : 3x – 2y + 1 = 0 và đường tròn (C) :
x^2 + y^2 - 2x + 4y -4 = 0
a. Tìm tọa độ A’ và phương trình (d’) lần lượt là ảnh của A và (d) qua phép tịnh tiến theo vectơ v = (– 2; 3)
b. Tìm phương trình đường tròn (C’) là ảnh của đường tròn (C) qua phép đối xứng trục là đường thẳng (D) : x – y = 0















