Giải phương trình sau dùng thuật toán Euclide 54x - 11y = 7
Dùng thuật toán Euclide giải phương trình 54x - 11y = 7
Giải phương trình Diophante 54x - 11y = 7 bằng thuật toán Euclide
Viết thuật toán (bằng cách liệt kê các bước) giải bài toán giải bất phương trình ax+b>0 với a,b là số thực. Sau đó viết chương trình (dùng NNLT Python) giải bài toán đó
Giải các hệ phương trình sau bằng phương pháp cộng đại số: 2 x - 11 y = - 7 10 x + 11 y = 31
Giải các hệ phương trình sau bằng phương pháp thế:
7 x - 3 y = 5 4 x + y = 2
7 x - 3 y = 5 1 4 x + y = 2 2
Từ (2) rút ra được y = -4x + 2.
Thế y = -4x + 2 vào phương trình (1) ta được :
7x – 3.(-4x+2) = 5 ⇔ 7x + 12x – 6 = 5 ⇔ 19x = 11 ⇔ 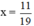
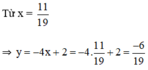
Vậy hệ phương trình có nghiệm duy nhất 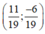
Bài 1:Viết thuật toán và chương trình giải phương trình bậc 2 ax^2+bx+c=0
Bài 2:viết thuật toán và viết chương trình giải phương trình bậc 1 ax+b=0
Bài 2:
Thuật toán:
B1: Nhập a,b
B2: Kiểm tra nếu a=0 và b=0 thì phương trình có vô số nghiệm
B3: Kiểm tra nếu a=0 thì phương trình vô nghiệm
B4: Kiểm tra nếu a khác 0 thì có nghiệm x=-b/a;
Viết chương trình:
Program HOC24;
var a,b: integer;
x: real;
begin
write('Nhap a; b: '); readln(a,b);
if a=0 and b=0 then write('Phuong trinh co vo so nghiem');
if a=0 then write('Phuong trinh vo nghiem');
if a<>0 then write('x=',-b/a:1:2);
readln
end.
Bài 1:
Thuật toán:
B1: Nhập a,b,c
B2: Tính \(\Delta\) = b2-4ac;
B3: Kiểm tra nếu \(\Delta\) >0 phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}\text{ }}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)
B4: Kiểm tra nếu \(\Delta\)<0 thì phương trình vô nghiệm
B5: Kiểm tra nếu \(\Delta\)=0 phương trình có 2 nghiệm kép \(x_1=x_2=-\dfrac{b}{2a}\)
Viết chương trình:
Program HOC24;
var a,b,c: integer;
x1,x2: real;
denta: longint;
begin
write('Nhap a; b; c: '); readln(a,b,c);
denta:=b*b-4*a*c;
if denta>0 then
begin
write('x1= ',(-b+sqrt(denta))/(2*a):1:2);
write('x2= ',(-b-sqrt(denta))/(2*a):1:2);
end;
if denta<0 then write('Phuong trinh vo nghiem');
if denta=0 then write('x= ',-b/2*a:1:2);
readln
end.
Dùng thuật tóan Euclide tìm UCLN ( 25n + 36; 9n + 13 ) và BCNN ( 25n +36; 9n + 13 ), ∀n ϵ N
Giải các hệ phương trình sau:
a.{2x-10y = -7
{10x + 11y = 31
b.{4x + 7y = 16
{4x - 3y = -24
a: Ta có: \(\left\{{}\begin{matrix}2x-10y=-7\\10x+11y=31\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10x-50y=-35\\10x+10y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-60y=-66\\2x-10y=-7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{11}{10}\\2x=-7+10y=-7+11=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{11}{10}\end{matrix}\right.\)
Với mô tả thuật toán giải phương trình bậc nhất ax + b = 0 ở mục Khởi động, em hãy tạo chương trình Scratch thể hiện thuật toán đó.
Sử dụng khối lệnh if else như sau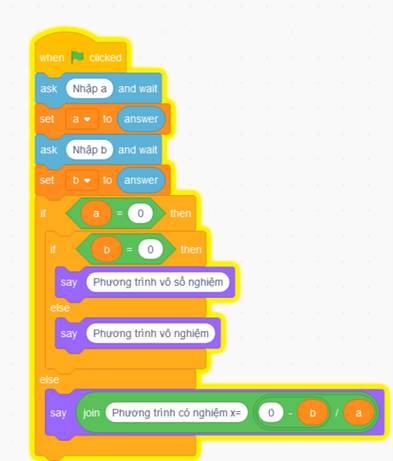
Thu được kết quả như sau: